В решении.
Объяснение:
Построить на одной координатной плоскости графики функций:
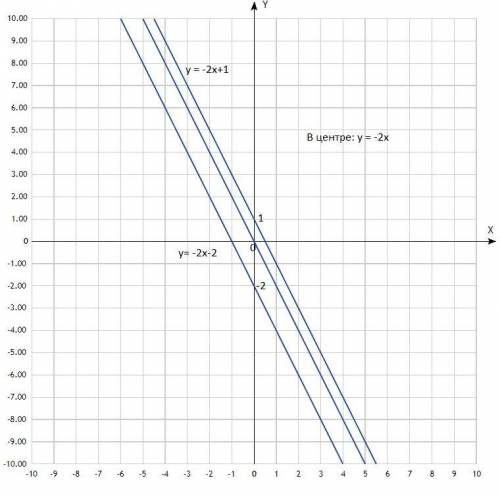
у= -2х, у= -2х+1, у= -2х-2.
Построить графики. Графики линейной функции, прямые линии. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
у= -2х у= -2х+1 у= -2х-2
Таблицы:
х -1 0 1 х -1 0 1 х -1 0 1
у 2 0 -2 у 3 1 -1 у 0 -2 -4
По вычисленным точкам построить прямые.
Вывод по построению: если коэффициенты перед х равны (k₁=k₂=k₃), графики данных линейных функций параллельны.
Объяснение:
1. 2x2 - 3x + 2 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-3)2 - 4·2·2 = 9 - 16 = -7
Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.
2. 3x2 - 3x - 6 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-3)2 - 4·3·(-6) = 9 + 72 = 81
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = -1
x2 = 2
3. 2x2 + 12x - 18 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = 122 - 4·(-2)·(-18) = 144 - 144 = 0
Так как дискриминант равен нулю то, квадратное уравнение имеет один действительный корень:
x = 3
4. x2 + x - 20 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = 12 - 4·1·(-20) = 1 + 80 = 81
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = -5
x2 = 4
5. -x2 + 5x - 6 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = 52 - 4·(-1)·(-6) = 25 - 24 = 1
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = 3
x2 = 2