Алгебра: Решите уравнение (2y-3)(3y+1)+2(y-5)(y+5)=2(1-2y)^2+6y

Решите уравнение
(2y-3)(3y+1)+2(y-5)(y+5)=2(1-2y)^2+6y

👇

Увидеть ответ

Ответ:

dimat123

25.07.2021

8 y^2 - 7 y - 53 = 2 (4 y^2 - y + 1)

8 y^2 - 7 y - 53 = 8y^2 - 2y + 2

- 7 y - 53 = -2 y + 2

-5y =55

y = -11

Добавлю для некоторых подробное решение, с самого начала, без сокращений, с комментариями

(2y-3)(3y+1)+2(y-5)(y+5)=2(1-2y)^2+6y

Подробное решение

6y^2 + 2y - 9y - 3 + 2(y^2 - 25) = 2(1 - 4y + 4y^2) + 6y

6y^2 + 2y - 9y - 3 + 2y^2 - 50 = 2 - 8y + 8y^2 + 6y

8y^2 - 7y - 53 = 8y^2 - 2y + 2 /сокращаем 8y^2

-7y - 53 = -2y + 2 /Перенесём известные в одну сторону, неизвестные в другую

-7y + 2y = 2 + 53

-5y = 55

y = -11

4,6(37 оценок)

Открыть все ответы

Ответ:

debiltrue

25.07.2021

№1

Пусть x-скорость лодки по течению, тогда y-скорость лодки против течения. Составим систему уравнений:

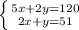
$\left \{ {{5x+2y=120} \atop {2x+y=51}} \right.$

Домножим нижнее уравнение на -2

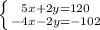
$\left \{ {{5x+2y=120} \atop {-4x-2y=-102}} \right.$

Решим методом сложения:

5x+2y-4x-2y=120-102

x=18

Подставим значение х во второе уравнение и найдем y:

2*18+y=51

36+y=51

y=51-36

y=15

Пусть скорость течения-x, а скорость лодки - y. Составим систему уравнений:

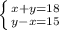
$\left \{ {{x+y=18} \atop {y-x=15}} \right.$

Решим методом сложения

x+y+y-x=32

2y=32

y=32/2

y=16

Подставим значение y в первое уравнение и найдем x:

x+16=18

x=18-16

x=2

ответ: скорость течения реки- 2км/ч. скорость лодки - 16 км/ч

№2

Пусть x- возраст отца, y-возраст сына

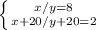
$\left \{ {{x/y=8} \atop {x+20/y+20=2}} \right.$

Выразим x из первого уравнения:

x/y=8

x=8y

Подставим значение x во второе уравнение:

8y+20/y+20=2

Перемножим методом креста:

2y+40=8y+20

-6y=-20

y=20/6

Выразим x:

x=8*20/6

x=80/3

Прибавим по 20 к x и y

x+20=80/3+20=140/3=46

y+20=20/6+20=140/6=23

ответ: Сыну 23 года, Отцу 46 лет.

Объяснение:

4,6(19 оценок)

Ответ:

stepnikitka

25.07.2021

Найдите целые отрицательные решения неравенств:

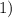
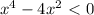
$x^4-4x^2\ \textless \ 0$
Рассмотрим функцию f(x)=x^4-4x^2

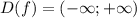
Её область определения: $D(f)=(-\infty;+\infty)$

Приравниваем функцию к нулю:
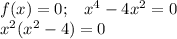
$f(x)=0;\,\,\,\,\, x^4-4x^2=0\\ x^2(x^2-4)=0$
Произведение равно нулю, если один из множителей равен нулю
$\left[\begin{array}{ccc}x^2=0\\x^2-4=0\end{array}\right\Rightarrow \left[\begin{array}{ccc}x_1=0\\ x_2_,_3=\pm 2\end{array}\right$

На интервале найдем решение неравенства

_+___(-2)___-___(0)___-___(2)___+___
Решением неравенства есть промежуток - $x \in (-2;0)\cup(0;2)$

Целое отрицательное число из промежутка: -1

ответ: -1.

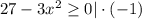
$27-3x^2 \geq 0|\cdot(-1)$
При умножении неравенства на отрицательное число, знак неравенства меняется на противоположный

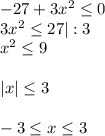
$-27+3x^2 \leq 0\\ 3x^2 \leq 27|:3\\ x^2 \leq 9\\ \\ |x| \leq 3\\ \\ -3 \leq x \leq 3$

Целые отрицательные числа промежутка: -3; -2; -1.

ответ: -3; -2; -1.

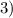
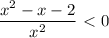
$\dfrac{x^2-x-2}{x^2} \ \textless \ 0$
Рассмотрим функцию
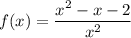
$f(x)= \dfrac{x^2-x-2}{x^2}$
Область определения:
$x\ne 0$
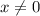
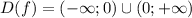
$D(f)=(-\infty;0)\cup(0;+\infty)$
Приравниваем функцию к нулю:
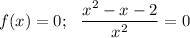
$f(x)=0;\,\,\,\, \dfrac{x^2-x-2}{x^2} =0$
Дробь обращается в 0 тогда, когда числитель равен нулю
x^2-x-2=0

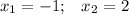
По т. Виета: $x_1=-1;\,\,\,\,\, x_2=2$

Найдем решение неравенства
___+___(-1)___-____(0)____-__(2)____+____
$x \in (-1;0)\cup(0;2)$ - решение неравенства

Целых отрицательных чисел - НЕТ

ответ: целых отрицательных чисел нет

$\dfrac{x^2+x}{x^2-3} \leq 0$
Рассмотрим функцию
$f(x)= \dfrac{x^2+x}{x^2-3}$
Область определения функции:
$x^2-3\ne 0\,\,\,\, \Rightarrow\,\,\,\,\,\, x\ne\pm \sqrt{3}$

$D(f)=(-\infty;- \sqrt{3} )\cup(- \sqrt{3} ; \sqrt{3} )\cup( \sqrt{3} ;+\infty)$

Приравниваем функцию к нулю
$\dfrac{x^2+x}{x^2-3} =0$
Дробь обращается в нуль, если числитель равен нулю
$x^2+x=0\\ x(x+1)=0\\ \left[\begin{array}{ccc}x=0\\ x+1=0\end{array}\right\Rightarrow \left[\begin{array}{ccc}x_1=0\\ x_2=-1\end{array}\right$

Вычислим решение неравенства:
__+___(-√3)__-__[-1]__+___[0]___-__(√3)__+____
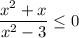
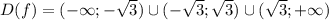
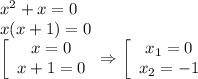
Решение неравенства: $x \in (- \sqrt{3} ;-1]\cup[0;\sqrt{3} )$

Целые отрицательные решения : -1

ответ: -1.

4,8(83 оценок)

Это интересно:

Семейная-жизнь

09.02.2020

Все, что вам нужно знать о последних неделях беременности...

Здоровье

05.05.2023

Как правильно лечить разрыв кисты яичника?...

Образование-и-коммуникации

18.04.2023

Как заставить коллегу перестать указывать вам, как делать вашу работу: советы по установлению границ, коммуникации и уверенности в себе...

Образование-и-коммуникации