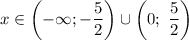Объяснение:
подставим x-координату точки в формулу у=9/x если получится у-координата то график проходит через точку иначе не проходит
(-1;9) 9/-1=-9 ≠ 9 не проходит
(-9:1) 9/-9=-1 ≠ 1 не проходит проходит
(-3;3) 9/-3=-3 ≠ 3 не проходит
(-4,5;2) 9/-4,5=-2 ≠ 2 не проходит
ответ график не проходит через эти точки
Примечание
можно без вычислений определить что график не проходит через эти точки. y=9/x это означает, что обе координаты должны быть одного знака, либо обе положительные либо обе отрицательные. У всех точек координаты разного знака значит график не проходит через эти точки
<!--c-->
Преобразим заданное уравнение:
x3+12x2−27x=a
С производной построим график функции y=x3+12x2−27x.
1. Введём обозначение f(x)=x3+12x2−27x.
Найдём область определения функции D(f)=(−∞;+∞).
2. Найдем стационарные и критические точки, точки экстремума и промежутки монотонности функции:
f′(x)=(x3+12x2−27x)′=3x2+24x−27.
Внутренние точки области определения функции, в которых производная функции равна нулю, назывём стационарными, а внутренние точки области определения функции, в которых функция непрерывна, но производная не существует, —критическими.
Производная существует всюду в области определения функции, значит, критических точек у функции нет. Стационарные точки найдем из соотношения f′(x)=0:
3x2+24x−27=0|÷3x2+8x−9=0D4=(b2)2−ac=822+9=25x1,2=−b2±D4−−√a=−82±25−−√1=−82±5x1=−82−5=−9x2=−82+5=1
Критические и стационарные точки делят реальную числовую прямую на интервалы с неизменным знаком производной. Чтобы определить знак производной, достаточно вычислить значение производной функции в какой-либо точке соответственного интервала.
Если производная функции в критической (стационарной) точке:
1) меняет знак с отрицательного на положительный, то это точка минимума;
2) меняет знак с положительного на отрицательный, то это точка максимума;
3) не меняет знак, то в этой точке нет экстремума.
Итак, определим точки экстремума:
При x<−9 имеем положительную производную (на этом промежутке функция возрастает); при −9<x<1 имеем отрицательную производную (на этом промежутке функция убывает). Значит, x=−9 — точка максимума функции. При −9<x<1 имеем отрицательную производную, при
Объяснение:
ОДЗ: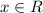
Найдем точки пересечения с осью абсцисс:
Нарисуем координатную прямую и отметим на ней точки пересечения с осью абсцисс, и найдем значение функции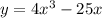
на каждом участке ("+" — если функция находится над осью абсцисс, "-" — если функция находится под осью абсцисс), подставляя в функцию число из промежутка (см. вложение).
Так как у нас неравенство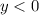
, то нас устроят промежутки со знаком "-", не включая точки пересечения с осью абсцисс.
ответ: