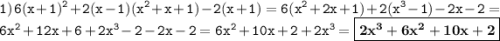
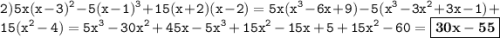
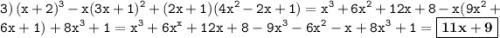
В решении.
Объяснение:
Пользоваться этими формулами:
D=b²-4ac = √D=
х₁=(-b-√D)/2a
х₂=(-b+√D)/2a
1. Решить уравнения:
1) x² +8x-13 = 0;
D=b²-4ac = 64+52=116 √D= √4*29 = 2√29;
х₁=(-b-√D)/2a
х₁=(-8 -2√29)/2
х₁= -4 - √29;
х₂=(-b+√D)/2a
х₂=(-8 + 2√29)/2
х₂= -4 + √29.
2) 2x²- 4x-17 = 0;
Разделить уравнение на 2 для упрощения:
x²- 2x - 8,5 = 0;
D=b²-4ac = 4 + 34 = 38 √D= √38 = √4*9,5 = √4*19/2 = 2√19/2;
х₁=(-b-√D)/2a
х₁=(2-2√19/2)/2
х₁=1-√19/2; 19/2 под корнем;
х₂=(-b+√D)/2a
х₂=(2+2√19/2)/2
х₂=1+√19/2; 19/2 под корнем;
3) 9x² +42x+49 =0;
D=b²-4ac = 1764 - 1764 = 0 √D=0
х=(-b±√D)/2a
х= -42/18
х= -7/3.
4) x² -10x+37 = 0;
D=b²-4ac = 100 - 148 = -48
D < 0
Уравнение не имеет действительных корней.
5) (3x+2)(x-4)=5;
Раскрыть скобки, привести подобные члены:
3х² - 12х + 2х - 8 - 5 = 0
3х² - 10х - 13 = 0
D=b²-4ac = 100 + 156 = 256 √D=
16
х₁=(-b-√D)/2a
х₁=(10-16)/6
х₁= -6/6
х₁= -1;
х₂=(-b+√D)/2a
х₂=(10+16)/6
х₂=26/6
х₂=13/3.
6) (3(х² - 1))/7 - (х + 9)/6 = (х + 6)/3
Умножить уравнение (все части) на 42, чтобы избавиться от дробного выражения, надписать над числителями дополнительные множители:
6*3(х² - 1) - 7*(х + 9) = 14*(х + 6)
Раскрыть скобки:
18х² - 18 - 7х - 63 = 14х + 84
Привести подобные члены:
18х² - 7х - 81 - 14х - 84 = 0
18х² - 21х - 165 = 0
Разделить уравнение на 3 для упрощения:
6х² - 7х - 55 = 0
D=b²-4ac = 49 + 1320 = 1369 √D=37
х₁=(-b-√D)/2a
х₁=(7-37)/12
х₁= -30/12
х₁= -2,5;
х₂=(-b+√D)/2a
х₂=(7+37)/12
х₂=44/12
х₂=11/3.
Проверка путём подстановки вычисленных значений х в уравнения показала, что данные решения удовлетворяют данным уравнениям.