![1)\; \; \int \sqrt{x}\cdot lnx\, dx=\Big[\; u=lnx,\; du=\frac{dx}{x},\; dv=\sqrt{x}, dx,\; v=\frac{2\, x^{3/2}}{3}\; \Big]=\\\\=uv-\int v\m du=\frac{2x^{3/2}}{3}\cdot lnx-\frac{2}{3}\int \frac{x^{3/2}}{x}\, dx=\frac{2\, \sqrt{x^3}}{3}\cdot lnx-\frac{2}{3}\int x^{1/2}\, dx=\\\\=\frac{2\, \sqrt{x^3}}{3}\cdot lnx-\frac{2}{3}\cdot \frac{2\, x^{3/2}}{3}+C=\frac{2\, \sqrt{x^3}}{3}\cdot lnx-\frac{4}{9}\cdot \sqrt{x^3}+C=\\\\=\frac{2\, \sqrt{x^3}}{3}\cdot (lnx-\frac{2}{3})+C\; ;](/tpl/images/1069/2227/80f98.png)
![2)\; \; \int sin(lnx)\, dx=\Big[\; t=lnx\; ,\; x=e^{t}\; ,\; dx=e^{t}\, dt\; \Big]=\int sint\cdot e^{t}\, dt=Q\\\\\\Q=\int sint\cdot e^{t}\, dt=\Big[\; u=sint\; ,\; du=cost\, dt\; ,\; dv=e^{t}\, dt\; ,\; v=e^{t}\; \Big]=\\\\=uv-\int v\, du=e^{t}\cdot sint-\int cost\cdot e^{t}\, dt=\Big[\; u=cost\; ,\; du=-sint\, dt\; ,\\\\dv=e^{t}\, dt\; ,\; v=e^{t}\; \Big]=e^{t}\cdot sint-\Big (e^{t}\cdot cost+\int sint\cdot e^{t}\, dt\Big)=\\\\=e^{t}\cdot (sint-cost)-\int sint\cdot e^{t}\, dt=e^{t}\cdot (sint-cost)-Q\; ;](/tpl/images/1069/2227/0b1f9.png)
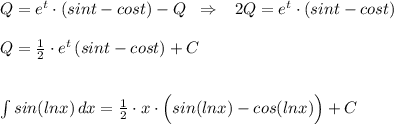
Задание № 4:
В двух корзинах 79 яблок, причём 7/9 первой корзины составляют зелёные яблоки, а 9/17 второй корзины - красные яблоки. Сколько красных яблок во второй корзине?
получаем, что яблок в первой корзине делится на 9, а число яблок во второй корзине делится на 17
9х+17у=79
х=1: 9+17у=79; 17у=70; у не целое
х=2: 18+17у=79; 17у=61; у не целое
х=3: 27+17у=79; 17у=52; у не целое
х=4: 36+17у=79; 17у=43; у не целое
х=5: 45+17у=79; 17у=34; у=2
х=6: 54+17у=79; 17у=25; у не целое
х=7: 63+17у=79; 17у=16; у<1
значит в первой корзине 9*5=45 яблок, во второй - 17*2=34, (9/17)*34=18 красных яблок
ответ: 18