![-\frac{\pi}{2}\leq arcsin(2-\frac{3x}{5})\leq \frac{\pi}{2}\\\\-\frac{\pi}{2}\cdot \frac{3}{4\pi }\leq \frac{3}{4\pi }arcsin(2-\frac{3x}{5})\leq \frac{\pi}{2}\cdot \frac{3}{4\pi }\\\\-\frac{3}{8}\leq \frac{3}{4\pi }arcsin(2-\frac{3x}{5})\leq \frac{3}{8}\\\\\frac{3}{4\pi }arcsin(2-\frac{3x}{5})\in [\, -\frac{3}{8}\, ;\, \frac{3}{8}\; ]](/tpl/images/1071/8653/74f85.png)
см, тогда второй катет - 
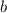см. Площадь прямоугольного треугольника равна 
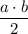, что составляет 210 см² или перепишем сразу 
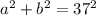
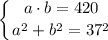
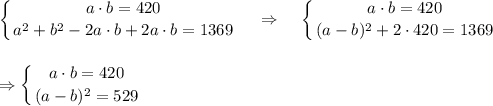
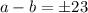. Тогда имеем несколько случаев.
, то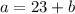 
и подставим в первое уравнение.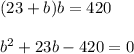
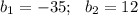см и корень 
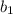не удовлетворяет заданному условию
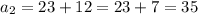см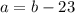
,то подставив в первое уравнение, получим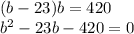
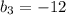
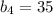см и корень 
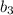не удовлетворяет условию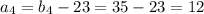
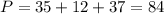см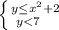
Нарисуем параболу у=х²+2, ветви вверх, вершина в точке (0,2) . Надо заштриховать область, расположенную ниже этой параболы.
Нарисуем прямую у=7, она проходит параллельно оси ОХ через точку (0,7) . Надо заштриховать область, расположенную ниже этой прямой. Так как неравенство у<7 строгое, то линия у=7 не входит в область, её рисуем штриховой линией.
Тогда область, соответствующая системе неравенств, будет та, которая получается в результате наложения штриховок. Верхняя граница этой области обведена зелёной линией.
