Упростить и решить при а=-2
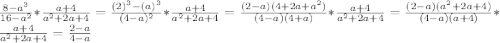
при а=-2
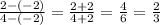
1,75
Объяснение:
S = x1(1-x2) + x2(1-x3) + x3(1-x4) + x4(1-x5) + x5(1-x6) + x6(1-x7) + x7(1-x1)
При условии: x1; x2; x3; x4; x5; x6; x7 ∈ [0; 1]
Очевидно, что при x1 = x2 = x3 = x4 = x5 = x6 = x7 = 0 будет S = 0
Точно также, при x1 = x2 = x3 = x4 = x5 = x6 = x7 = 1 будет S = 0
Так как выражение симметрично относительно переменных, то любую переменную можно заменить на любую другую.
Это значит, что максимум будет достигнут при равных значениях всех переменных.
Сумма будет максимальной при x1 = x2 = x3 = x4 = x5 = x6 = x7 = 0,5
S = 0,5*0,5 + 0,5*0,5 + 0,5*0,5 + 0,5*0,5 + 0,5*0,5 + 0,5*0,5 + 0,5*0,5 =
= 0,25*7 = 1,75
(8-a^3)(a+4) 8-a^3 8-a^3
= = =
(4-a)(4+a)(a^2+2a+4) (4-a)(a^2+2a+4) 4a^2+8a+16-a^3-2a^2-4a
8-a^3
=
-a^3-2a^2+4a+16
если а=-2,то 8-a^3 8-(-2)^3 8+8 16
= = == -4
-a^3-2a^2+4a+16 -(-2)^3-2(-2)^2+4(-2)+16 -8-4-8+16 -4