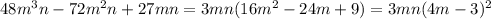Прежде чем продолжить, давайте разберемся с определениями, чтобы убедиться, что мы на одной волне.
Степень в математике - это операция, которая выражает умножение числа (называемого основанием) на само себя несколько раз. В данном случае используется степень с показателем 3.
Произведение - это операция, при которой мы умножаем два или больше чисел друг на друга.
Теперь приступим к решению вашего вопроса.
Нам нужно представить выражение (5b^2)^3 в виде произведения. Для этого нам нужно применить свойство степени, которое гласит: (ab)^n = a^n * b^n. Отсюда мы можем выразить исходное выражение в виде (5^3)*(b^2)^3.
Теперь давайте приступим к пошаговому решению:
1. Возведение в степень 5^3:
5^3 = 5 * 5 * 5 = 125
2. Возведение в степень b^2:
(b^2)^3 = b^(2*3) = b^6
Привет! Конечно, я помогу тебе разобраться с этим вопросом. Для начала, давай разберемся, что такое прямые и ребро.
Прямая - это бесконечно длинная и прямая линия, которая не имеет начала или конца. Ребро - это отрезок, соединяющий две вершины полиэдра (в нашем случае куба).
Теперь нужно понять, какие прямые скрещиваются с ребром BC. Чтобы это сделать, давай рассмотрим наш куб поближе.
Вершины нашего куба обозначены буквами A, B, C и D, а для удобства добавлены индексы 1. Ребро BC соединяет вершину B с вершиной C.
Теперь давай проведем прямые, которые скрещиваются с ребром BC. Мы можем провести прямую через ребро, если эта прямая проходит через любую точку на ребре BC.
Прямые, скрещивающиеся с ребром BC, будут перпендикулярны ребру BC и содержать точки на ребре. Чтобы найти такую прямую, нам нужно знать хотя бы одну точку на ребре BC и направление прямой.
Давай найдем одну точку на ребре BC. Вершина B находится на ребре BC, поэтому можем начать с нее.
Теперь нужно определить направление прямой. Направление определяется двумя параллельными плоскостями, и проходящей через ребро BC. По нашим правилам, каждая прямая должна быть перпендикулярна ребру BC.
Поскольку у нас есть только одно ребро нашего куба, я могу провести только одну прямую. Она будет перпендикулярна ребру BC и будет содержать точку B. Давай я проведу эту прямую на схеме нашего куба.
1)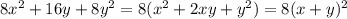
2)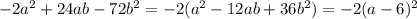
3)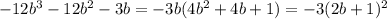
4)