мне кажется что первое
1
Когда число возводится в степень с натуральным показателем, то имеется в виду, что оно умножается само на себя столько раз, каков показатель степени:
43 = 4 × 4 × 4; 26 = 2 × 2 × 2 × 2 × 2 × 2
Когда же показатель степени равен 1, то при возведении имеется всего лишь один множитель (если тут вообще можно говорить о множителях), и поэтому результат возведения равен основанию степени:
181 = 18; (–3.4)1 = –3.4
Но как в таком случае быть с нулевым показателем? Что на что умножается?
Попробуем пойти иным путем. Известно, что если у двух степеней одинаковые основания, но разные показатели, то основание можно оставить тем же самым, а показатели либо сложить друг с другом (если степени перемножаются), либо вычесть показатель делителя из показателя делимого (если степени делятся):
32 × 31 = 32+1 = 33 = 3 × 3 × 3 = 27
45 ÷ 43 = 45–3 = 42 = 4 × 4 = 16
А теперь рассмотрим такой пример:
82 ÷ 82 = 82–2 = 80 = ?
Что если мы не будем пользоваться свойством степеней с одинаковым основанием и произведем вычисления по порядку их следования:
82 ÷ 82 = 64 ÷ 64 = 1
Вот мы и получили заветную единицу. Таким образом нулевой показатель степени как бы говорит о том, что число не умножается само на себя, а делится само на себя.
И отсюда становится понятно, почему выражение 00 не имеет смысла. Ведь нельзя делить на 0.
Можно рассуждать по-другому. Если имеется, например, умножение степеней 52 × 50 = 52+0 = 52, то отсюда следует, что 52 было умножено на 1. Следовательно, 50 = 1.
Объяснение:
Это правило
, 
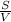= 4 часа — время, потраченное легковой машиной на путь. 
ответ: =1 при х=0.
Объяснение:
(x³-4x)/(2x²-4x)=x*(x²-4)/(2x*(x-2))=(x-2)(x+2)/(2*(x-2))=(x+2)/2=(x/2)+1.
(x/2)+1≥1
х/2≥0 |×2
x≥0 ⇒
x=0
(0/2)+1=0+1=1.