ЗА Знайти суму 2-го та 3-го членів геометричної прогресії, в якій четвертий член більший, ніж другий, на 120, а третій більший першого на 30

👇

Увидеть ответ

Ответ:

Aron91

08.05.2022

ответ: b₂+b₃=40.

Объяснение:

b₂+b₃=?

{b₄-b₂=120 {b₁q³-b₁q=120 {b₁q*(q²-1)=120

{b₃-b₁=30 {b₁q²-b₁=30 {b₁*(q²-1)=30

Разделим первое уравнение на второе:

q=4

b₁*(4²-1)=30

b₁*(16-1)=30

15*b₁=30 |÷15

b₁=2

b₂=2*4=8

b₃=2*4²=2*16=32

b₂+b₃=8+32=40.

4,8(38 оценок)

Ответ:

Zhora231

08.05.2022

Объяснение:

b₄=b₁q³; b₂=b₁q

b₄-b₂=120

120=b₁q³-b₁q=b₁q(q²-1)

b₃=b₁q²

b₃-b₁=30

30=b₁q²-b₁=b₁(q²-1)

4=120/30=b₁q(q²-1)/[b₁(q²-1)]=q⇒q=4

b₂=b₁q=2·4=8

b₃=b₂q=8·4=32

b₃+b₂=32+8=40

=120/(4-1)=120/3=40

4,8(14 оценок)

Открыть все ответы

Ответ:

Кристалина12

08.05.2022

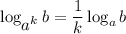1) а) По свойству $\log_\big{a^k}b=\dfrac{1}{k}\log_ab$ имеем , что
$\log_\big{ \frac{1}{2} }16=\log_\big{2^{-1}}16=-\log_\big{2}16=-\log_\big{2}2^\big{4}=-4$

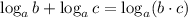б) Используя свойство $\log_ab+\log_ac=\log_a(b\cdot c)$ , получим что
$51+\log53=\log10^{51}+\log53=\log(53\cdot 10^{51})$

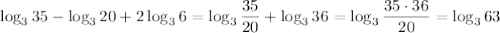
в) $\log_335-\log_320+2\log_36=\log_3 \dfrac{35}{20} +\log_336=\log_3 \dfrac{35\cdot 36}{20} =\log_363$

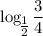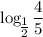
Задание 2. Сравнить числа: $\log_\big{ \frac{1}{2} } \dfrac{3}{4}$ и $\log_\big{ \frac{1}{2} } \dfrac{4}{5}$

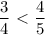Поскольку $\dfrac{3}{4} \ \textless \ \dfrac{4}{5}$ , то в силу монотонности функции( 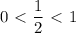$0\ \textless \ \dfrac{1}{2} \ \textless \ 1$ функция убывающая) имеем что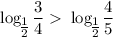
$\log_\big{ \frac{1}{2} } \dfrac{3}{4}\ \textgreater \ \log_\big{ \frac{1}{2} } \dfrac{4}{5}$

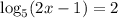
Задание 3. Решить уравнение $\log_5(2x-1)=2$
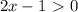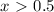
ОДЗ уравнения: $2x-1\ \textgreater \ 0$ откуда $x\ \textgreater \ 0.5$
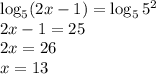
$\log_5(2x-1)=\log_55^2\\ 2x-1=25\\ 2x=26\\ x=13$

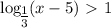
Задание 4. Решить неравенство $\log_\big{ \frac{1}{3} }(x-5)\ \textgreater \ 1$
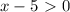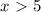
ОДЗ: $x-5\ \textgreater \ 0$ откуда $x\ \textgreater \ 5$
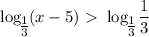
$\log_\big{ \frac{1}{3} }(x-5)\ \textgreater \ \log_\big{ \frac{1}{3} } \dfrac{1}{3}$
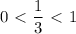Поскольку основание $0\ \textless \ \dfrac{1}{3} \ \textless \ 1$ , функция убывающая, то знак неравенства меняется на противоположный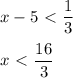
$x-5\ \textless \ \dfrac{1}{3} \\ \\ x\ \textless \ \dfrac{16}{3}$

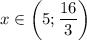
С учетом ОДЗ получим окончательный ответ $x \in \bigg(5; \dfrac{16}{3}\bigg)$

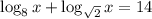
Задание 5. Решить уравнение $\log_8x+\log_{ \sqrt{2} }x=14$
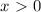
ОДЗ уравнения $x\ \textgreater \ 0$
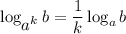Используя свойство $\log_\big{a^k}b=\dfrac{1}{k}\log_ab$ , получим что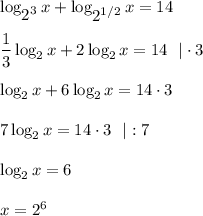
$\log_\big{2^3}x+\log_\big{2^{1/2}}x=14\\ \\ \dfrac{1}{3} \log_2x+2\log_2x=14~~|\cdot 3\\ \\ \log_2x+6\log_2x=14\cdot 3\\ \\ 7\log_2x=14\cdot 3~~|:7\\ \\ \log_2x=6\\ \\ x=2^6$

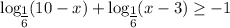
Задание 6. Решить неравенство $\log_\big{ \frac{1}{6} }(10-x)+\log_\big{ \frac{1}{6} }(x-3)\geq -1$
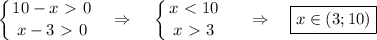
ОДЗ $\displaystyle \left \{ {{10-x\ \textgreater \ 0} \atop {x-3\ \textgreater \ 0}} \right. ~~\Rightarrow~~~ \left \{ {{x\ \textless \ 10} \atop {x\ \textgreater \ 3}} \right. ~~~~\Rightarrow~~~ \boxed{x\in (3;10)}$

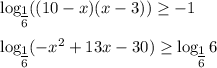
$\log_\big{ \frac{1}{6} }((10-x)(x-3))\geq -1\\ \\ \log_\big{ \frac{1}{6} }(-x^2+13x-30)\geq \log_\big{ \frac{1}{6} }6$
В силу монотонности функции логарифма имеем что
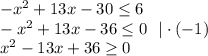
$-x^2+13x-30\leq 6\\ -x^2+13x-36\leq 0~~|\cdot(-1)\\ x^2-13x+36\geq 0$
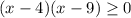$(x-4)(x-9)\geq 0$ (*)
Решением последнего неравенства (*) есть $x \in (-\infty;4]\cup[9;+\infty)$

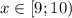С учетом ОДЗ $x \in [9;10)$ - ОТВЕТ.

Задание 7. Решить неравенство $\log_3^2x-2\log_3x \leq 3$
ОДЗ неравенства $x\ \textgreater \ 0$
Представим левую часть неравенства в следующем виде:
$\log_3^2x-2\log_3x+1\leq 4\\ \\ (\log_3x-1)^2\leq 4\\ \\ |\log_3x-1|\leq 2\\ \\ -2\leq \log_3-1\leq 2~~|+1\\ \\ -1\leq \log_3x\leq 3$

Имеем совокупность неравенств $\left[\begin{array}{ccc}\log_3x\geq -1\\ \log_3x\leq 3\end{array}\right~~~\Rightarrow~~~~~ \left[\begin{array}{ccc}x \geq \dfrac{1}{3}\\ x\leq 27 \end{array}\right$

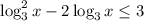
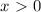
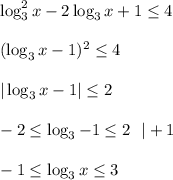
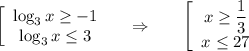
И с учетом ОДЗ мы получим ответ $x \in \bigg[\dfrac{1}{3} ;27\bigg].$

4,5(43 оценок)

Ответ:

Котёнок0007

08.05.2022

1. Январь: А₁=106
Декабрь: А₁₂ - ?
d=3
S₁₂-?
A₁₂=A₁+3*11=106+33=139 (шт) - изготовили в декабре
S₁₂=(A₁+A₁₂) * 12 =6*(106+139)=6*245=1470 (шт) - изготовили за год.
2
ответ: 139 шт, 1470 шт.

2. Аn=2*3^n
A₁=2*3¹=6
A₂=2*3²=2*9=18
A₃=2*3³=2*27=54
В геометрической прогрессии квадрат каждого члена, отличного от первого и последнего, равен произведению соседних с ним членов:
А₂²=А₁ * А₃
18²=6*54
324=324
Условие выполняется, значит заданная последовательность есть геометрическая последовательность.

4,6(19 оценок)

Это интересно:

31.01.2021

Как бороться со стрессом с помощью еды...

Хобби-и-рукоделие

20.02.2022

Как просто и быстро сделать стильные шорты из старых джинсов: 5 шагов к идеальному летнему гардеробу...

Мир-работы

27.04.2021

5 способов не отвлекаться на Интернет во время работы...

Кулинария-и-гостеприимство

31.01.2022