В решении.
Объяснение:
Решить графически систему уравнений:
у = х² - 7
у = |x|
Первый график - парабола со смещённым центром, ветви направлены вверх.
Второй график - график функции модуля (значения у всегда > 0).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х² - 7 у = |x|
Таблицы:
х -4 -3 -2 -1 0 1 2 3 4 х -3 -2 -1 0 1 2 3
у 9 2 -3 -6 -7 -6 -3 2 9 у 3 2 1 0 1 2 3
По вычисленным точкам построить графики.
Согласно графиков, координаты точек пересечения:
(-3,2; 3,2); (3,2; 3,2).
Решения системы уравнений: (-3,2; 3,2); (3,2; 3,2).
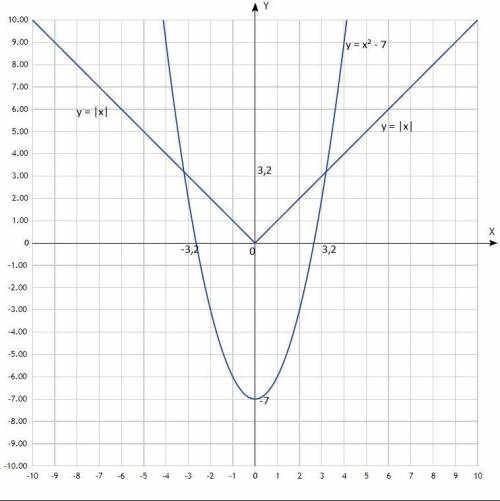
В решении.
Объяснение:
Решить графически систему уравнений:
у = х² - 7
у = |x|
Первый график - парабола со смещённым центром, ветви направлены вверх.
Второй график - график функции модуля (значения у всегда > 0).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х² - 7 у = |x|
Таблицы:
х -4 -3 -2 -1 0 1 2 3 4 х -3 -2 -1 0 1 2 3
у 9 2 -3 -6 -7 -6 -3 2 9 у 3 2 1 0 1 2 3
По вычисленным точкам построить графики.
Согласно графиков, координаты точек пересечения:
(-3,2; 3,2); (3,2; 3,2).
Решения системы уравнений: (-3,2; 3,2); (3,2; 3,2).

Объяснение:
1) √2(√2-√18)= √2√2-√2√18=√4-√36=2-6=-4
√2(√2-√18)=√2(√2-3√2)=√2(-2√2)=-2(√2)²=-2·2=-4
2) √7(4√7+√28-√175)=√7(4√7)+√7√28-√7√175=4(√7)²+√196-√1225=
=28+14-35=7
√7(4√7+√28-√175)=√7(4√7+2√7-5√7)=√7·√7=7
3)(2√6+√12)(√96-3√3)-2√72=√12(√2+1)√3(4√2-3)-2√72=
=6(√2+1)(4√2-3)-2√72=6(8-3√2+4√2-3)-12√2=6(5+√2)-12√2=30-6√2