A) cosx≤1/2 ⇒ -1≤cosx≤1/2 ⇒ x∈ [2πk+π/3; (2(k+1)π -π/3] Подробнее: cosx убывающая в области [0;π] от 1 до -1,т. е. у нас в обл. [π/3 ;π] от 1/2 до -1 cosx возрастает в обл. [π;2π] , у нас [π;2π-π/3] или [π;5/3·π] ⇒ x∈[π/3; π] U [π; 5/3·π] =[ π/3; 5π/3] и учитывая периодичность : x∈ [2πk +π/3 ; 2πk+5π/3] k∉N
b) sinx>√2/2 sinx≥0 в промежутке [0;π] . В [0;π/2] возрастает от 0 до 1 и убывает от 1 до 0 в обл. [π/2;π]. ⇒ π - π/4 <x< π/4 , т.е. x∈(π/4 ; 3π/4) ответ: x∈ (π/4 + 2πk ; 3π/4 + 2πk) k∉N
1) x²-7x=0
x(x-7)=0
x=0 или x=7
2) 4x²-25=0
4x²=25
2x=±5
x=±2.5
3) (x+2)(x-3)-(x-5)(x+5)=x²-x
x²-x-6-(x²-25)=x²-x
-6-x²+25=0
-x²=-19
x=±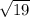
4) x²-4x-32=0
x=-4 или x=8
5) 4x²+28x+49=0
D=28²-4*4*49=784-784=0
x=-28/8=-3.5
6) (4x-3)²+(3x-1)(3x+1)=9
16x²-24x+9+9x²-1=9
25x²-24x-1=0
D=24²+4*25=576+100=676
√D=26
x=(24-26)/50=-1/25
или x=(24+26)/50=1