Тема урока. Характеристики случайной величины. Математическое ожидание и дисперсия
1. числовые характеристики с определениями
2. Выписать примеры
3. Решить до 15-30
1) задание из презентации
Найдите среднее арифметическое, размах и моду ряда чисел:
а) 16, 22, 16, 13, 20, 15;
б) -21, -33, -35, -19, -20, -22;
в) -4, -6, 0, 4, 0, 6, 8, -12.
2) Дисперсия случайной величины Х равна 3. Найдите D(Y), где
а) Y = 3X:
б) Y = X + 5;
Домашнее задание (1)гл.11(3)
• Выучить все определения, методы вычисления, свойства числовых характеристик.
Задача 1. Дано распределение случайной величины Z
Значения – 4 0 6
Вероятность 0,3 0,5 0,2
Вычислить дисперсию этой случайной величины.
Задача 2. Дисперсия случайной величины Х равна 3. Найдите D(Y), где
в) y – 4X;
г) Y = 2X – 1;
д) Y = 5 – 3X;
е) Y = – 5X – 7.
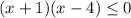
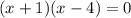
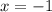
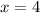
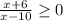
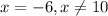
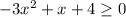
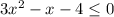
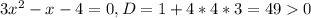
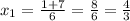
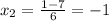
При x≤-1 - функция положительная
При -1≤x≤4 - функция отрицательная
При x≥4 - функция положительная
выбираем те интервалы, где функция положительная (неотрицательная) - это x≤-1 и x≥4
ответ: x∈(-бесконечность; -1]U[4; +бесконечность)
2)
При x≤-6 - функция положительная
При -6≤x<10 - функция отрицательная
При x>10 - функция положительная
выбираем те интервалы, где функция положительная (неотрицательная):
x∈(-бесконечность; -6]U(10; +бесконечность)
3) подкоренное выражение должно быть неотрицательным:
-1≤x≤4/3