Алгебра: Знайти значення виразу: (18y-6x)/9, якщо 5x-5y=1stion

Знайти значення виразу: (18y-6x)/9, якщо 5x-5y=1stion

👇

Увидеть ответ

Ответ:

Nadya1111111111111

23.03.2022

Так как выражения не пропорциональны, то однозначного решения нет.

Можно только найти зависимость от одной из переменных.

В числителе первого выражения вынесем за скобку 9:

(9(2y-(2/3)x))/9 = 2у - (2/3)х.

Из второго выражения определяем зависимость:

5x-5y=1, откуда у = х - 0,2.

Это значение можно подставить в первое выражение и получаем его зависимость от переменной х:

2*(х - 0,2) - (2/3)х = 2х - (2/3)х - 0,2 = (4/3)х - 0,2.

ответ: (18y-6x)/9 = (4/3)х - 0,2 если 5x-5y=1.

4,5(95 оценок)

Открыть все ответы

Ответ:

ЧакН0рис

23.03.2022

1. а) значение аргумента равно 3, тогда значение функции:

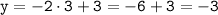
$\tt y=-2\cdot 3+3=-6+3=-3$

б) Согласно условию значение функции равно 5, то есть, 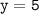$\tt y=5$ , то значение аргумента найдем, решив следующее уравнение:

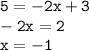
$\tt 5=-2x+3\\ -2x=2\\ x=-1$

в) Подставляя координаты точки В в график уравнения, получим

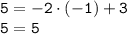
$\tt 5=-2\cdot(-1)+3\\ 5=5$

Раз выполняется тождество, следовательно, график 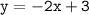$\tt y=-2x+3$ проходит через точку В(-1;5).

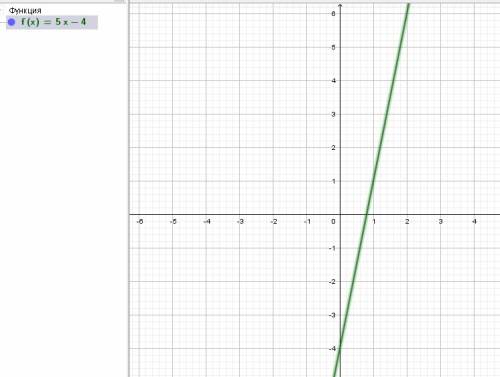
2. Графиком линейной функции является прямая. Для построения прямой достаточно взять две точки, например: 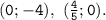$\tt (0;-4),~(\frac{4}{5} ;0).$

а) значению аргумента 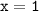$\tt x=1$ соответствует значение функции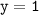 $\tt y=1$

б) значению функции 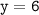$\tt y=6$ соответствует значение аргумента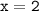 $\tt x=2$

3. Точки пересечения с осью координат Х. График функции пересекает ось Х при 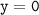$\tt y=0$ , значит нужно решить уравнение:

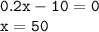
$\tt 0.2x-10=0\\ x=50$

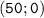$\tt (50;0)$ - точка пересечения графика с осью ОХ.

Точки пересечения с осью координат У. График пересекает ось У, когда 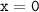$\tt x=0$ , то есть, подставляя х=0 в график уравнения, получим

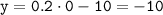
$\tt y=0.2\cdot 0-10=-10$

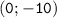$\tt(0;-10)$ - точка пересечения графика с ось ОY.

4. Раз график функции 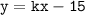$\tt y=kx-15$ проходит через точку 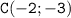$\tt C(-2;-3)$ , значит значение 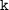$\tt k$ найдем, подставив координаты точки C, имеем

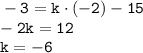
$\tt -3=k\cdot(-2)-15\\ -2k=12\\ k=-6$

1)функция задана формулой y=-2x+3. определите: а) значение функции если значение аргумента равно 3 б

4,8(22 оценок)

Ответ:

33даник747

23.03.2022

а) x²-64<0
1. Переносим 64 и меняем знак, число становится положительным.
x²<64
2. Избавляемся от степени. 64 это 8 во второй степени.
x<8
Получаем диапазон меньше 8. Чертим график, выделяем часть до числа 8. Точка будет пустой, так как знак неравенства строгий.
Получаем х∈(-∞,8).
ответ: (-∞;8)

б) (х+2)(х+4)<0
1. Корни уравнения известны, -4 и -2
2. Решаем по методу интервала.
Располагаем числа на графике, расставляем знаки поочередно (+ - +)
Получаем отрицательное значение в промежутке от -4 до -2, это и будет нашим ответом, т.к. знак неравенства отрицательный. Точки будут пустыми, знак строгий.
Получаем х∈(-4;-2).
ответ: (-4;-2)

в) х²-6x-7≤0
1. Решаем квадратичное уравнение, находим корни.
а=1; b= (-6); c= (-7)
D= b²-4ac = (-6)²-4×1×(-7) = 36+28=64
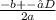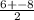
x₁,₂= $\frac{-b+-√D}{2a}$ = $\frac{6+-8} {2}$
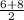x₁= $\frac{6+8} {2}$ = 7
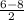x₂= $\frac{6-8} {2}$ = -1
2. Решаем по методу интервала.
Располагаем числа на графике, расставляем знаки поочередно (+ - +)
Получаем отрицательное значение в промежутке от -1 до 7, это и будет нашим ответом, т.к. знак неравенства отрицательный. Точки буду закрашенными, а скобки квадратными, т.к. знак неравенства нестрогий (≤).
Получаем х∈[-1;7].
ответ: [-1;7]

Надеюсь

Решите неравенство: а)х^2-64< 0 б)(х+2)(х+4)< 0 в)х^2-6х-7< или равно 0 решение с подробнос