Решение начнем с того, что перенесем все члены уравнения в одну сторону:
sin^2 (3x) = cos^2 (3x) – 1
cos^2 (3x) – sin^2 (3x) – 1 = 0.
Обратим внимание на разницу первых двух членов. Эту разницу можно свернуть в более короткую и удобную форму по формуле косинуса двойного угла, которая записывается следующим образом:
cos (2x) = cos^2 (x) – sin^2 (x).
В качестве аргумента в нашем случае выступает аргумент 3х. Запишем уравнение, свернув разницу первых двух членов по выше упомянутой формуле:
cos (2 * 3x) – 1 = 0
cos (6x) – 1 = 0.
Перепишем полученное уравнение в более удобной форме:
cos (6x) = 1.
Решим полученное тригонометрической уравнение любым из доступных Если косинус от любого аргумента равен единице, то аргумент этой функции равен 2 * пи * n. В данном случае аргумент косинуса равен 6х:
6x = 2 * пи * n.
Осталось вычислить значение переменной х. для этого разделим обе части уравнения на 6:
x = (пи * n ) / 3
x = пи / 3 * n.
ответ. x = пи / 3 * n, n – любое целое число.
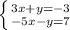
Перечёркиваем +y и -y,остальное слаживаем,получим уравнение:
-2x = 4
x= 4 : (-2)
x = -2
Если x = -2, то
3*(-2) + y = -3
-6 + y = -3
y = 3
ответ: ( -2;3)
2)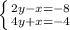
Перечёркиваем +x и -x, слаживаем остальное и получаем уравнение:
6y = -12
y = -12 : 6
y= -2
Если y= -2, то
2 *(-2) - x = -8
-4 - x = -8
-x = -4
x = 4
ответ: (4;-2)
3)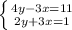
Перечёркиваем -3x и +3x, слаживаем остальное и получаем уравнение:
6y = 12
y = 2
Если y= 2, то
2 * 2 + 3x = 1
4 + 3x = 1
3x = -3
x = -1
ответ:(-1;2)
4)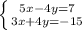
Перечёркиваем -4y и +4y, слаживаем остальное и получаем уравнение:
8x = -8
x = -1
Если x = -1, то
5 * (-1) - 4y = 7
-5 - 4y = 7
-4y = 12
y = -3
ответ: (-1;-3)
а) z(z+3y)
б) 3x(x2+2z)
в) y2(1+y5z)
г) x3(-1z3+1)
д)a2c2(a+c)
е)2b4(2ab+3c)
после букв цифры это степени
Объяснение: