а = 3, в = 4, с = 5. Треугольник прямоугольный, т.к 5² =3² + 4²
Биссектриса внутреннего угла тр-ка делит противолежащую углу сторону на части, пропорциональные прилегающим сторонам, т.е гипотенуза с поделена на отрезки: х, прилегающий к стороне а и (с-х), прилегающий к стороне b.
а:a1 = b:b1
3:х = 4:(5-x)
15 - 3x = 4x
7x = 15
a1 = x = 15/7
b1 = 5-x = 5 - 15/7 = 20/7
Сама биссектриса равна:
Lc = √(a·b - a1·b1)
Lc = √(3·4 - 15/7· 20/7)= √(12 - 300/49) = √(588/49 - 300/49) = √(288/49) =
12√2/7
ответ: 12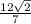
В решении.
Объяснение:
Построить график функции
y=2x² - 2
Указать:
1) Область определения функции;
2) Множество значений функции;
3) Те значения x, при которых y > 0.
Приравнять уравнение к нулю и решить как квадратное уравнение.
2x² - 2 = 0
2х² = 2
х² = 2/2
х² = 1
х = ±√1
х = ±1.
График функции - парабола со смещённым центром, пересекает ось Ох в точках (-1; 0) и (1; 0) - нули функции.
Построить график. Придать значения х, подставить в уравнение, вычислить значения у, записать в таблицу.
Таблица:
х -3 -2 -1 0 1 2 3
у 16 6 0 -2 0 6 16
1. Указать область определения.
Это проекция графика на ось Ох, значения х, при которых функция существует, обозначение D(f) или D(у).
По графику видно, что область определения ничем не ограничена, х может быть любым.
Запись: D(у) = х∈R (значения х - множество всех действительных чисел).
2) Указать множество значений функции.
Множество значений данной функции может быть ограничено только вершиной параболы, обозначение: E(f) или E(у).
Согласно графика, ордината (значение у) вершины параболы = -2, это значение является ограничением, верх параболы не ограничен, поэтому множество значений функции от у= -2 до + бесконечности.
Запись: E(у) = (-2; +∞).
3) Указать значения x, при которых y > 0.
Согласно графика, значения х, при которых у > 0 (график выше оси Ох) от - бесконечности до -1 и от 1 до + бесконечности.
Запись: у > 0 при х∈(-∞; -1)∪(1; +∞).