Вот накалякал. Разбирайся :)
xy/(x+y) = 5
xz/(x+z) = 7
yz/(y+z) = 9
xy = 5x + 5y
xz = 7x + 7z
yz = 9y + 9z
x(y-5) = 5y
x = 5y/(y-5)
5yz/(y-5) = 35y/(y-5) + 7z
5yz = 35y + 7z * (y-5)
5yz = 35y + 7yz - 35z
2yz + 35y = 35z
y(2z + 35) = 35z
y = 35z/(2z + 35) = z/(2z/35 + 1)
35z^2/(2z + 35) = 315z/(2z + 35) + 9z
35z^2 = 315z + 9z*(2z + 35)
35z^2 = 315z + 18z^2 + 315z
17z^2 = 630z
z=630/17
y = 35*630/(2*630/17 + 35)/17 = 35*630/(1260 + 595) = 22050/1855 = 630 / 53
x = 5*630/(630/53 - 5)/53 = 5*630/((630/53 - 5)*53) = 5*630/365 = 630/73
Рассмотрим указанный диапазон натуральных чисел как расширенный натуральный ряд (то есть такой, куда входит 0). Разобьём этот ряд на пары. Получим:
0;999999999
1;999999998
2;999999997
3;999999996
...и так далее.
Одно число (1000000000) останется без пары.
Из составленного понятно, что сумма цифр в одной паре равна: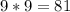 .
.
Так как мы разбили ряд на две равные части, количество пар будет равно:
Зная это, умножим сумму цифр в одной паре на количество пар и добавим 1, так как одно число у нас осталось без пары.
ответ: 40500000001