Координаты точки пересечения можно найти методом вычитания:
а) чтобы найти переменную , достаточно вычесть от верхней части системы нижнюю, тогда получится , найдем координату , подставим значение х в любую часть системы: , следовательно точка пересечения этих прямых будет находится по координатам
б) , искомый ответ будет
в) тут возникает противоречие, если прямые вычесть, то мы не сможем найти или , или же будет , что не является верным, значит прямые не будут пересекаться, они являются параллельными
г) тут уже можно сразу найти , искомый ответ будет
ответ: а), б), в)Нет решения, г)
Примечание: Если в г была система такая , то это это две прямые, которые совпадают и ответом будет бесконечное множество.
√7 + √10 и √3 + √19 Возведём в квадрат: 7 + 2√70 + 10 и 3 + 2√57 + 19 17 + 2√70 и 22 + 2√57 Перенесём 17 в одну сторону, а 2√59 в другую: 22 - 17 и 2√70 - 2√57 5 и 2√70 - 2√57 Возведём ещё раз в квадрат: 25 и 4·70 - 4√3990 + 4·59 25 и 516 - 4√3990 Перенесём 516 в другую сторону: 25 - 516 и -4√3390 -491 и -√63840 -√241081 и -√63840 Второе число больше первого, т.к. оба числа отрицательные, а второе больше по модулю. ответ: второе число больше.
Объяснение:
Координаты точки пересечения можно найти методом вычитания:
а)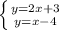
чтобы найти переменную 
, достаточно вычесть от верхней части системы нижнюю, тогда получится 
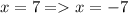, найдем координату 
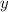, подставим значение х в любую часть системы: 
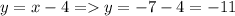, следовательно точка пересечения этих прямых будет находится по координатам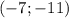 
б)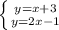
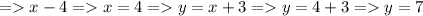, искомый ответ будет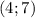 
в)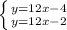
тут возникает противоречие, если прямые вычесть, то мы не сможем найти 
или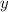 
, или же будет 
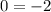, что не является верным, значит прямые не будут пересекаться, они являются параллельными
г)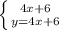
тут уже можно сразу найти 
, искомый ответ будет 
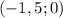
ответ: а)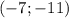
, б)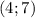
, в)Нет решения, г)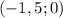
Примечание: Если в г была система такая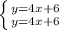
, то это это две прямые, которые совпадают и ответом будет бесконечное множество.