Введите здесь ваше решить уравнения с модулями: i x-3i=2 ixi+1=7 i 3x=2 i-4=0

👇

Увидеть ответ

Ответ:

борщ7

16.09.2022

1)Ix-3I=2

$\left \{ {{x-3=2} \atop {x-3=-2}} \right$

$\left \{ {{x=5} \atop {x=1}} \right$

2)IxI+1=7

IxI=6

$\left \{ {{x=6} \atop {x=-6}} \right$

3)I3x+2I-4=0

I3x+2I=4

$\left \{ {{3x+2=4} \atop {3x+2=-4}} \right$

$\left \{ {{3x=2} \atop {3x=-6}} \right$

$\left \{ {{x=2/3} \atop {x=-2}} \right$

4,7(24 оценок)

Открыть все ответы

Ответ:

lol2710

16.09.2022

1) a+b+c=0 => a+b=-c => (a+b)³=(-c)³ => a³+3a²b+3ab²+b³=-c³ =>
=> a³+b³+c³=-(3a²b+3ab²) => a³+b³+c³=-3ab(a+b) => a³+b³+c³=-3ab(-c) =>
=> a³+b³+c³=3abc
2) Обратное утверждение:
Если a³+b³+c³=3abc, то a+b+c=0 (думаю, имеется в виду, что a+b+c обязательно будет равно 0, и не существует других вариантов).
Из утверждения следует, что c³-3abc+a³+b³=0. Допустим, известны числа a и b. Тогда c³-3abc+a³+b³=0 является кубическим уравнением относительно c. Как известно, любое кубическое уравнение с рациональными коэффициентами имеет ровно три корня (необязательно действительных). Отсюда следует, что при фиксированных a и b и при 3-х вариантах c получится три варианта для суммы a+b+c, одним из которых является a+b+c=0.
Таким образом, пункт 1 является верным. Пункт 2 не является верным.
Найдем другие два варианта для c.
Известно, что в уравнении c³-3abc+a³+b³=0 одним из решений является c=-(a+b), так как при подстановке в уравнение получится тождество. Разложим левую часть уравнения на скобки:
c³-3abc+a³+b³=(a+b+c)(c²-c(a+b)+a²-ab+b²).
Решим уравнение c²-c(a+b)+a²-ab+b²=0 относительно c:
D=(-(a+b))²-4(a²-ab+b²)=a²+2ab+b²-4a²+4ab-4b²=-3(a²-2ab+b²)=-3(a-b)²≤0
c1,2=((a+b)+-√3(a-b)*i)/2, где i²=-1, i - мнимая единица.
Если D=0, то a=b, а выражение для c примет такой вид: c=(a+b)/2=(a+a)/2=a. Получим, что в этом случае a=b=c, а сумма a+b+c=3a для любого a.
Если D<0, то c1=(a+b)/2+i√3(a-b)/2,
c2=(a+b)/2-i√3(a-b)/2.
А возможные варианты для суммы станут такими:
a+b+c=a+b+(a+b)/2+i√3(a-b)/2=3(a+b)/2+i√3(a-b)/2,
или
a+b+c=a+b+(a+b)/2-i√3(a-b)/2=3(a+b)/2-i√3(a-b)/2

4,4(93 оценок)

Ответ:

софия731

16.09.2022

ответ: 8

Объяснение:

Добрый вечер!

Согласно правилам шахмат, ладья может ходить только по горизонтали и вертикали.

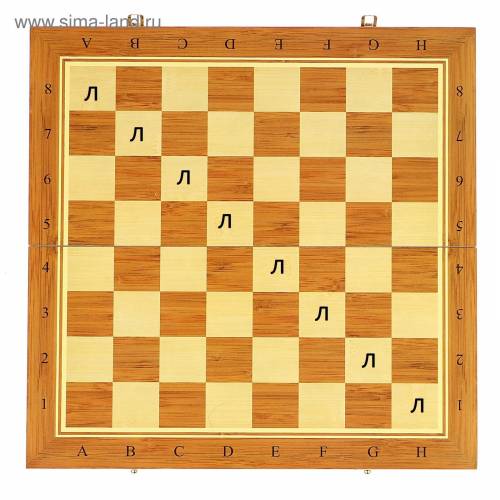
Если поставить, например, 8 ладей вдоль главной диагонали, то они не будут бить друг друга. (cмотрите рисунок)

Предположим, что можно расставить 9 ладей так, чтобы они не били друг друга.

Пусть мы расставили первые 8 ладей по этому правилу, но тогда в каждой вертикали данной доски может быть не более одной ладьи, а поскольку ладей 8, то все 8 вертикалей уже заняты, но тогда 9-ая ладья в любом случае попадает на уже занятую вертикаль, а значит находится под боем.

Таким образом, мы пришли к противоречию, расставить 9 и более ладей по такому правилу невозможно.

Значит, максимальное число ладей равно 8.

Если вам понравился ответ, cделай его лучшим!