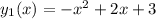 (1)
(1)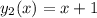 (2)
(2)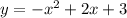 (1)
(1)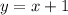 (2)
(2)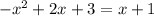
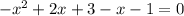
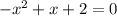 (3)
(3)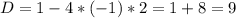
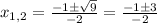
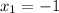
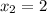
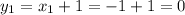
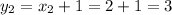
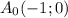

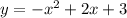 в параболу
в параболу  .
.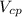 будет равен:
будет равен: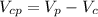 (4)
(4)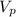 объем фигуры ограниченной, параболами и плоскостью перпендикулярной плоскости рисунка и проходящей через прямую
объем фигуры ограниченной, параболами и плоскостью перпендикулярной плоскости рисунка и проходящей через прямую 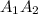 .
.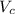 ? , объем конуса ограниченного прямыми и той же плоскостью проходящей через
? , объем конуса ограниченного прямыми и той же плоскостью проходящей через 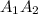
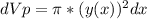
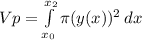 (5)
(5)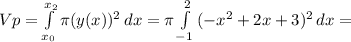
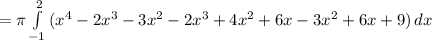
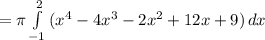 (6)
(6)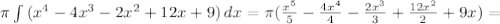
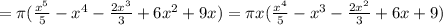 (7)
(7)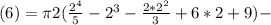
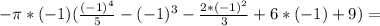
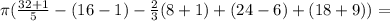
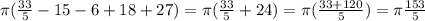 (8)
(8)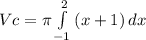 (9)
(9)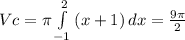 (10)
(10)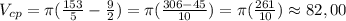
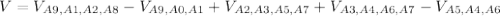
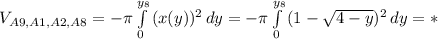
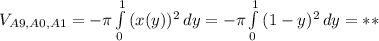

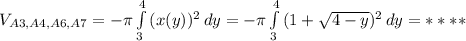

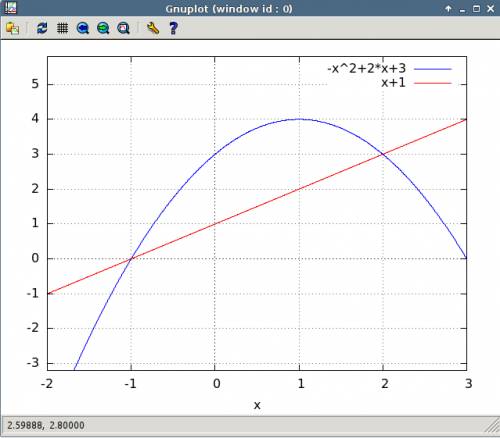
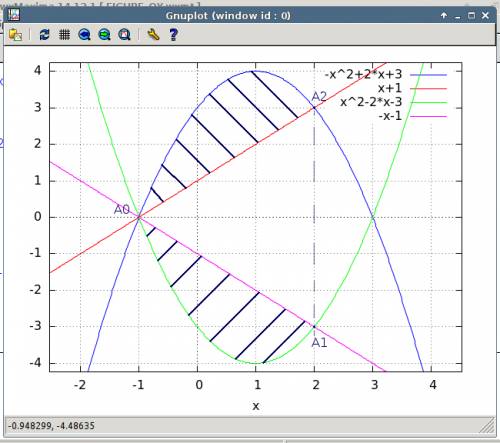
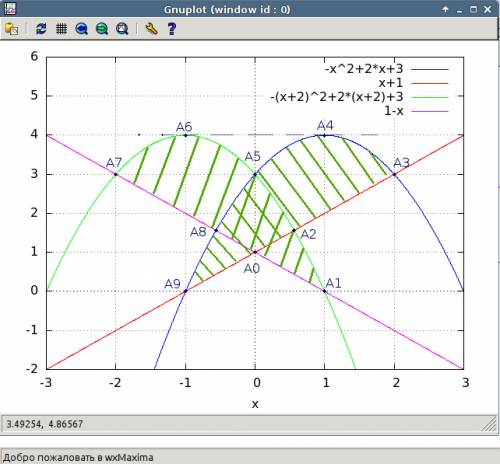
Объяснение:
а) f'(x)=8*(1/8)*x^7+4*(1/2√x)-5*(-1/x²)+7*1/x=x^7+2/√x+5/x²-5/x
б)f'(x)=(2/3)*3x²-6/2√x+4*(-1/x²)-5*(1/x)=2x²-3/√x-4/x²-5/x