Сначала мы пишем систему и смотрим на коэффициенты при х и у.
В данном случае, особой разницы нет, поэтому останавливаемся на коэффициентах при х. В первом уравнении коэффициент при х равен 4, а во втором 3. Нам надо, чтобы при почленном сложении двух уравнений сумма коэффициентов при х равнялась нулю. Этого можно добиться искусственно, если первое уравнение домножить на 3, а второе уравнение домножить на (-4) (данная операция обозначена вертикальными "палочками", после которых стоит знак умножения на нужное нам число
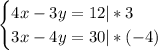
Получаем следующую систему:
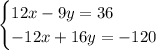
Теперь складываем уравнения "почленно", т.е. иксы с иксами, игреки с игреками, свободные члены со свободными членами. В результате получаем:
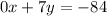
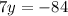
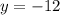
Осталось найти х. Для этого найденное значение у=-12 подставим в любое из первоначальных уравнений, например, в первое:
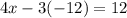

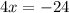

Осталось записать ответ. Допускаются следующие записи:
х=-6, у=-12 или (-6;-12)
задача - найти радиус окружности, описанной вокруг квадрата, то есть дна бассейна.
нетрудно заметить, что радиус этот совпадает с половиной диагонали того самого квадрата. Вот ее и будем искать.
диагонали квадрата равны и пересекаются под прямым углом, а значит - искомая половина диагонали - катет прямоугольного равнобедренного треугольника, гипотенузой которого является сторона квадрата.
Зная гипотенузу по теореме Пифагора легко подсчитаем катет, а значит,
найдем сторону квадрата - и катет (он же радиус, он же высота подвешенной лампочки) у нас в кармане!
приступим:
сторона квадрата - корень из площади = корень из 32 = 4 корня из двух
осталось посчитать упоминавшийся ранее катет, он же искомый радиус:
2r в квадрате = квадрат гипотенузы = 32
r = корень из 32 деленный на 2 = два корня из двух
это все!
Лампа висит на высоте 2 корня из двух [метров]
Ура!)