Для того чтобы исключить иррациональность из знаменателя дополнительный множитель берём равный иррациональному числу.
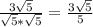(дополнительный множитель 
)
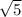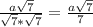(дополнительный множитель 
)
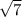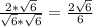(дополнительный множитель 
)
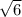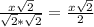(дополнительный множитель 
)
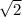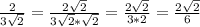(дополнительный множитель )
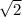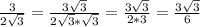(дополнительный множитель 
)
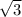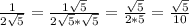(дополнительный множитель )
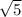Для того чтобы исключить иррациональность из знаменателя нужно использовать формулу сокращенного умнажения, а именно
a²-b²=(a-b)(a+b) дополнительный множитель должен быть либо a-b или a+b.
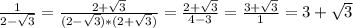
(остальное в фото)
Дополнительный множитель это число, которое нужно умножить на числитель и знаменатель. Причём значение дроби не меняется.
Окружность с центром в т. O и D = 68. Хорда AB.
Расстояние OM = 30 от т. O до прямой AB.
Найти:AB - ?
Решение:Заметим, что OM ⊥ AB (так как OM - это расстояние от т. О до прямой AB - длина перпендикуляра из точки О к прямой AB).
Пусть отрезок OM лежит на радиусе OC рассматриваемой окружности. Тогда OC, как радиус, перпендикулярный хорде, пересекает эту хорду ровно в ее середине: AM = BM.
Рассмотрим прямоугольные треугольники, равные по первому признаку (или же по двум катетам OM = OM и AM = BM): ΔAOM = ΔBOM.
OA = OB = D / 2 = 68 / 2 = 34, как радиусы.
OM = 30, по условию.
Применим теорему Пифагора, например, к ΔAOM:
AM² + OM² = AO²
AM² = AO² - OM²
AM² = 34² - 30²
AM² = 256
AM = 16
Значит:
AB = AM + BM = AM + AM = 16 + 16 = 32.
Задача решена!
ответ: 32.