ну смотри.
Возьмём в пример это:
(а+4)(6+а)
Мы должны умножать дугой: а×6=6а, а×а=а², 4×6=24, 4×а=4а.
Я прикреплю фото, чтобы было понятнее.
ответом будет являться: 6а+а²+24+4а.
Но ответ не окончательный, убираем подобные: 6а и 4а.
ответ: 10а+а²+24.
Выражение в виде произведения многочленов.
Пример:
а(m-3)+b(m-3)
В данном случае общим множителем является многочлен m-3. Поэтому выносим его в начало, а множители за скобками складываем и умножаем;
(m-3)(a+b)
Метод группировки.
Метод группировки - это разложение многочлена на множители, объединив в группы его члены.
Пример:
2ас+2bc+5am+5bm
Сгруппировать члены этого многочлена нужно так, чтобы слагаемые в каждой группе имели общий множитель.
2ас+2bc+5am+5bm=(2ac+2bc)+(5am+5bm)=
=2c(a+b)+5m(a+b)=(a+b)(2c+5m).
Ничего сложного нет, нужно это только понять.)
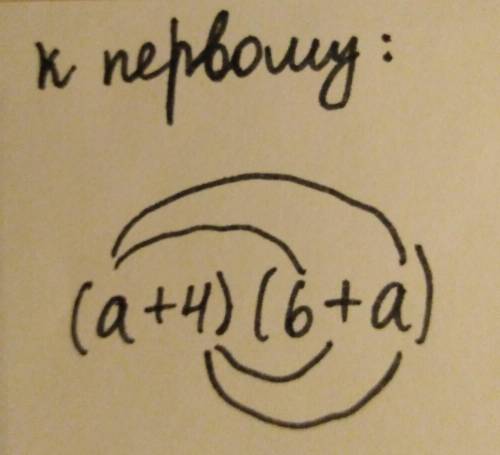
Применим формулу разности квадратов
(2х² - х - 7 + 5х + 1) * (2х² - х - 7 - 5х - 1) = 0
(2х² +4х - 6) * (2х² - 6х - 8) = 0
Приравняв каждую скобку к 0, получим два уравнения
2х² +4х - 6 = 0 и 2х² - 6х - 8 = 0
Решим первое
2х² + 4х - 6 = 0
D = 4² - 4 * 2 * 6 = 16 - 48 = - 32 отрицательный, корней нет
Решим второе
2х² - 6х - 8 = 0
Сократив на 2, получим уравнение
х² - 3х - 4 = 0
D = 9 - 4 * 1 * (-4) = 9 + 16 = 25
√D = √25 = 5
х₁ = (3 + 5)/2 = 8/2 = 4 - наибольший корень
х₂ = (3 - 5)/2 = -2/2 = - 1 - наименьший корень
|x₁ - x₂| = |4 - (-1)| = |4+1| =5
ответ: 5