1. У системі координат намалюй трикутник ABC з координатами вершин:
A(−1;−1) , B(−5,4;−1) , C(−1;−5,4)
2. Намалюй трикутник A1B1C1 , отриманий при повороті трикутника ABC навколо початку координат на 180° .
3. Намалюй трикутник A2B2C2 , отриманий у симетрії трикутника A1B1C1 відносно прямої x=0.
Визнач координати:
A2(
;
) ;
B2(
;
) ;
C2(
;
) .
Яким чином можна було б із трикутника ABC одразу отримати трикутник A2B2C2 ?
симетрією відносно осі Ox
симетрією відносно прямої y=0
центральною симетрією відносно початку координат
поворотом на 180 градусів навколо початку координат
паралельним перенесенням на вектор (1;1)
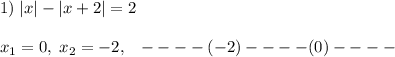
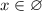 .
.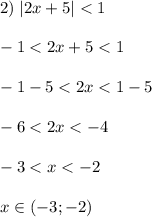
Расматриваем 3 интервала и в каждом интервале подсчитаем знаки выражений ,стоящих под модулем. Затем будем раскрывать модули в 3-х случаях в зависимости от рассматриваемого интервала.
Для |x|: - - - - - -(-2) - - - - (0) + + + +
Для |x+2|: - - - - - -(-2) + + +(0) + + + +
a) xЄ(-беск, -2] ---> -x-(-x-2)=2, 2=2 верно для любых х на этом промежутке
б) хЄ(-2;0] ---> -x-(x+2)=2, -2х-2=2, х=-2 (не входит в данный промежуток)
в) хЄ(0,беск) ---> x-(x+2)=2, -2=2 неверное раавенство --->
ответ: хЄ(-беск; -2] .
Если |x|<a, то -а<x<a .