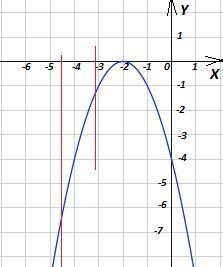
y = -x² - 4x - 4 = -(x + 2)² - квадратичная функция, график - парабола, ветви направлены вниз (-1 < 0). Вершина параболы в точке (-2;0) - из уравнения параболы.
A) x ≤ -2; Так как вершина параболы в точке (-2; 0) и ветви направлены вниз, значит, на интервале x∈(-∞; -2] функция монотонно возрастает.
Б) Максимум функции в точке (-2; 0). Абсцисса вершины не принадлежит заданному интервалу : x₀ = -2 ∉ [-4,5; -3,1]
Значения функции на границах интервала
y(-4,5) = -(-4,5 + 2)² = -(-2,5)² = -6,25 - наименьшее значение
y(-3,1) = -(-3,1 + 2)² = -(-1,1)² = -1,21 - наибольшее значение
Пусть по плану требовалось x машин с грузоподъемностью (60/x) тонн каждая.
В связи с ремонтом взяли (x+1) машину с грузоподъемностью 60/(x+1) тонн каждая.
Так как в каждую машину стали загружать на 3 тонны меньше,
составим уравнение:
60/x - 60/(x+1) = 3
ОДЗ:
x(x+1) от сюда следует, что
x ≠ 0 ; x ≠ - 1
60(x+1) - 60x = 3 *x(x+1)
60x + 60 - 60x = 3x² + 3x
60 = 3x² + 3x
3x² + 3x - 60 = 0 |÷3
x² + x - 20 = 0
D(дискриминант) = 1² - 4*1*(-20) = 1 + 80 = 81 = 9²
x₁ = (-1 - 9)/(2*1) = -10/2 = -5 не удовл. условию задачи
x₂ = (-1 +9)/(2*1) = 8/2 = 4 машины - требовалось по плану
4 + 1 = 5 машин - использовали на самом деле.
60: 4 = 15 тонн - грузоподъемность по плану.
1. Вначале требовалось 4 машины .
2. На самом деле использовали 5 машин.
3. Планировалось перевозить 15 тонн груза на одной машине