Объяснение:
24.124
найдем разность арифметической прогрессии
d = 4,5 - 4,9 = -0.4
a₁ +(-0.4)(n-1) < 0
4.9 -0.4n +0.4 < 0
-0.4n < -5.4
n > 13.5
т.к. n должно быть целым числом, то наш ответ n = 14
ответ
начиная с 14-го члена члены арифметической прогрессии будут отрицательными
24.125
разница между соседними членами должна быть одинаковой
m+3-(m²+1) = m+3 -(m²+1)
m+3 -m²-1 = m²+1 -3m +1
-2m² +4m =0 m₁ = 0 m₂=2
значение указанных выражений будут членами арифметической прогрессии при m = 0 -1; 1; 3 a₁ = -1 d= 2
при m = 2 получим прогрессию 5; 5 ;5 a₁ = 5 d =0
24.126
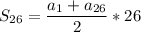
a₁ = 0.2*1+5 = 5.2
a₂₆ = 0.2*26 +5 = 10.2
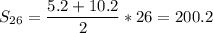
24.127
1) найдем d
a₁₄ = a₁ +13d = 6 + 13d = 45 13d = 39 d = 3
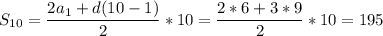
2)
из двух известных членов найдем а₁ и d
a₆ = a₁ +5d = 34 a₁ = 34-5d
a₁₄ = a₁ +13d =34 -5d +16d = -54 11d = -88 d = -8 тогда a₁ = 74
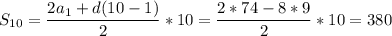
V(л) = 16,5 км/час - скорость лодки
V(р) - скорость реки
V(л) + V(р) - скорость лодки по течению реки
V(л) - V(р) - скорость лодки против течения реки
S - путь в один конец
Тогда время будет:
по течению:
t(1) = S / (V(л) + V(р)) = 2ч 20мин . = 2 1/3 часа = 7/3 часа
Отсюда
S = 7/3 * (V(л) + V(р))
по течению:
t(2) = S / (V(л) - V(р))= 2ч 20мин - 28 мин = 7/3 часа - 28/60 часа=7/3 - 7/15 часа = 35/15 - 7/15 = 28/15 часа
Отсюда
S = 28/15 * (V(л) - V(р))
приравнять S в обоих случаях и решить уравнения
я думаю будет как то так на этом примеры ты должен понять решение
Пример 1. В урне 3 белых и 8 черных шаров. Наудачу отобраны 5 шаров. Найти вероятность того, что среди них окажется ровно 2 белых шара.
Подставляем в формулу (1) значения: K=10, N−K=8, итого N=10+8=18, выбираем n=5 шаров, из них должно быть k=2 белых и соответственно, n−k=5−2=3 черных. Получаем:
P=C210⋅C38C518=45⋅568568=517=0.294.
Пример 2. В урне 5 белых и 5 красных шаров. Какова вероятность вытащить наудачу оба белых шара?
Здесь шары не черные и белые, а красные и белые. Но это совсем не влияет на ход решения и ответ.
Подставляем в формулу (1) значения: K=5 (белых шаров), N−K=5 (красных шаров), итого N=5+5=10 (всего шаров в урне), выбираем n=2 шара, из них должно быть k=2 белых и соответственно, n−k=2−2=0 красных. Получаем:
P=C25⋅C05C210=10⋅145=29=0.222.
Пример 3. В корзине лежат 4 белых и 2 черных шара. Из корзины достали 2 шара. Какова вероятность, что они одного цвета?
Здесь задача немного усложняется, и решим мы ее по шагам. Введем искомое событие
A= (Выбранные шары одного цвета) = (Выбрано или 2 белых, или 2 черных шара).
Представим это событие как сумму двух несовместных событий: A=A1+A2, где
A1= (Выбраны 2 белых шара),
A2= (Выбраны 2 черных шара).
Выпишем значения параметров: K=4 (белых шаров), N−K=2 (черных шаров), итого N=4+2=6 (всего шаров в корзине). Выбираем n=2 шара.
Для события A1 из них должно быть k=2 белых и соответственно, n−k=2−2=0 черных. Получаем:
P(A1)=C24⋅C02C26=6⋅115=25=0.4.
Для события A2 из выбранных шаров должно оказаться k=0 белых и n−k=2 черных. Получаем:
P(A2)=C04⋅C22C26=1⋅115=115.
Тогда вероятность искомого события (вынутые шары одного цвета) есть сумма вероятностей этих событий: