![g(x)=\sqrt[3]{3x-1}=(3x-1)^{\frac{1}{3}}\\\\g'(x)=\frac{1}{3}\cdot (3x-1)^{-\frac{2}{3}}\cdot (3x-1)'=\frac{1}{3\sqrt[3]{(3x-1)^2}}\cdot 3\\\\g'(\frac{2}{3})=\frac{1}{\sqrt[3]{(2-1)^2}}=1](/tpl/images/0408/1971/483fb.png)
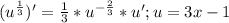
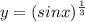,то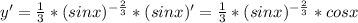
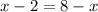
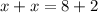
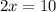
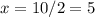
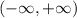, но не принадлежит 
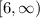, ![(-\infty, 0]](/tpl/images/0408/1975/03e35.png)
, 
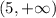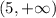.. Тут круглая скобка перед 5 означает, что точка x=5 исключена "вырезана" из интервала, а квадратная означает, что точка включена в интервал. Вот, например x=5 принадлежит интервалу 
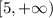. Если обе крайние точки принадлежат интервалу, то насколько мне помнится его называют "отрезок".
а) х/у=3/5 х=0,6у х=0,6у х=6,12
х+у=16,32 0,6у+у=16,32 у=16,32/1,6 у=10,2
б) х/у=3/5 х=0,6у х=0,6у х=0,525
х-у=0,35 0,6у-у=0,35 у=-0,35/0,4 у=0,875