А) Точки пересечения с осями : (0, -2) и (5,0).
Б) Точка не принадлежит графику.
Объяснение:
А)
Функция х - 2,5 у - 5=0. имеет неприведенный вид. Для начала выразим у:
у =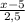 
Пересечение с осями определяется приравниванием х и у к нулю:
Если х = 0, то у = -2 график пересекает ось у
Если у = 0, то х = 5 график пересекает ось х
Точки пересечения с осями : (0, -2) и (5,0)
Б)
Чтобы проверить, принадлежит ли точка графику функции подставим вместо х --> -5,5 , а вместо у --> -2,6
-2,6 =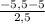 
выражение неверно , а значит точка не принадлежит графику.
y'(x) = - 25 x^4 + 9 x^2 = 9 x^2 - 25 x^4;
9 x^2 - 25 x^4= 0;
9x^2 ( 1 - 25x^4 / 9) = 0;
(3x)^2 * ( 1- 5x/2) (1+ 5x/2) = 0;
x1 = 0; Четный корень, так как он повторяется
x2 = - 2,5;
x3 = 2,5.
Теперь методом интервалов определим знаки производной
y' + - четн - +
- 2,5 02,5x
y возр убыв убыв возр.
max min
Находим знаки производной на этих промежутках , подставляя числа из промежутков в в уравнение производной y'=9 x^2 - 25 x^4;
значение х= 3 - это число из самой правой области (0т 2,5 до бескон-ти). Дальше чередуем, не забываем о том, что через точку х=0 проходим, не меняя знак.
Таким образом , точка минимума - это точка х = 2,5. Именно в ней производная меняет знак с плюса на минус.
У Вас получилось 2 точки минимума, потому что Вы наверняка не учли, что здесь 4 корня, 2 из которых одинаковые (х=0 и х =0). При переходе через корень четной степени( в данном случае второй степени) знак не меняется