Если каждое слагаемое делится на некоторое число, то и вся сумма делится на это число.
Если одно слагаемое делится на некоторое число, а другое слагаемое не делится на это число, то и вся сумма не делится на это число.
1.
Пусть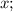 
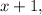
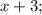
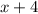- пять последовательных натуральных чисел, тогда их сумма равна:
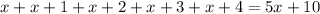
Очевидно, что каждое слагаемое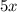 
и 
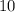делится на 5, а это означает, что вся сумма делится на 5.
Доказано.
2.
Пусть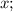 
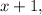
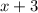- четыре последовательных натуральных числа, тогда их сумма равна:
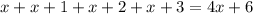
Очевидно, что первое слагаемое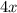 
делится на 4, а второе слагаемое 
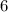не делится на 4, это означает, что вся сумма не делится на 4.
Доказано.
3.
Пусть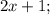 
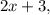
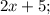
- четыре последовательных нечётных натуральных числа, тогда их сумма равна:
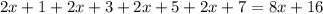
Очевидно, что каждое слагаемое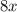 
и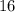 
делится на 8, а это означает, что вся сумма делится на 8.
Доказано.
4.
Пусть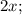 
; 
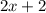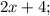
- четыре последовательных чётных натуральных числа, тогда их сумма равна:
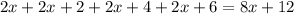
Очевидно, что каждое слагаемое 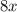и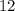 
делится на 4, а это означает, что вся сумма делится на 4.
Доказано.
Время затраченное грузовиком и легковым автомобилем на весь путь t(г) и t(a) соответственно. По условию t(a)=t(г)-1.
Найдём скорость автомобился и грузовика из формулы v=S/t:
v(a)=S/t(a)=S/(t(г)-1)
v(г)=S/t(г).
По условию сказано, что при движении навстречу друг другу они затратили 1 час и 12 минут, т.е. t(3)=1,2 ч.
Так как они двигались на встречу друг к другу, то общая скорость v(o)=v(a)+v(г).
Тогда весь путь равен S=v(o)t(3).
Подставляем значение общей скорости:
S=(v(a)+v(г))t(3)
Подставляем значения скоростей, которые нашли ранее:
S=(S/(t(г)-1) + S/t(г))×t(3)
Выносим S за скобки и сокращаем:
1=(1/(t(г)-1) + 1/t(г))×t(3)
Приводим всё к общему знаменателю внутри скобок и получаем уравнение:
t(г)^2-3.4t(г)+1.2=0
Решая уравнение находим время которон затратил грузовик на весь путь t(г)=3ч. (Корень 0.4 не подойдет, т.к. тогда получится, что время автомобилч на дорогу отрицательно)
Ну а время автомобиля на дорогу t(a)=3-1=2