№1.
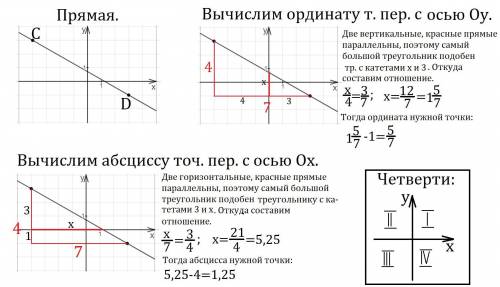
Отметим данные точки и проведём через них прямую.
Прямая пересекает ось Oy в точке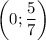 
; ось Ox в точке (1,25;0). Подробнее смотри в приложении.
№2.
Точка M(x;y):
расположена в 1 четверти, если x>0 и y>0;
расположена во 2 четверти, если x<0 и y>0;
расположена в 3 четверти, если x<0 и y<0;
расположена в 4 четверти, если x>0 и y<0.
Точка A(-87;89) расположена во 2 четверти т.к. -87<0 и 89>0.
Точка B(3,5;2) расположена в 1 четверти т.к. 3,5>0 и 2>0.
Точка C(0,1;-0,001) расположена в 4 четверти т.к. 0,1>0 и -0,001<0.
Точка D(-1,25;-3,48) расположена в 3 четверти т.к. -1,25<0 и -3,48<0.
ответ: ymin=y(-4)=-164
Объяснение:
Найдите наименьшее значение функции у = х³ - 5х² + 8х + 12 на отрезке [-4;1].
Найдем значение функции на границах отрезка
у(-4) = (-4)³ - 5·(-4)² +8·(-4) + 12 = -64 - 80 - 32 + 12 = -164
у(1) = 1³ - 5·1² +8·1 + 12 = 1 - 5 + 8 + 12 = 16
Найдем производную функции
у' =(х³ - 5х² + 8х + 12)' = (х³)' - (5х²)' + (8х)' + (12)' = 3x² - 10x +8
Найдем критические точки приравняв производную к нулю
3x² - 10x + 8 = 0
D = (-10)² - 4·3·8 = 100 - 96 = 4
x₁ = (10-2)/(2·3) = 8/6 = 4/3 ≈ 1,33
x₂ = (10+2)/(2·3) = 12/6 = 2
Найденные точки не входят в данный отрезок поэтому значения функции в них находить не будем.
Функция на отрезке монотонна и возрастает. Минимальное значение функции находится в точке x = -4 y(-4) = -164
![РЕШИТЬ.Найдите наименьшее значение функции у=х^3-5х^2+8х+12 на отрезке [-4;1].](/tpl/images/1353/3405/90f6a.jpg)
1) {X=3.
{y=6
2) {X=3
{y=2
Объяснение:
{y=2x
{x-2x=-3
{-x=-3
{y=2x
{x=3
{y=2x
{X=3
{y=6
2) 2x=6;
X=3;
3+y=5;
y=2
{X=3
{y=2