Дана система уравнений:
{9x^2-42xy+52y^2-6y=265
{3x-7y-11=0.
Заданная система решается методом подстановки.
Из второго уравнения находим у = (3/7)х - (11/7) и подставляем вместо переменной у в первое уравнение.
Вычисление довольно громоздкое.
Результат: х1 = (-31/3), у1 = -6.
х2 = (67/3), у2 = 8.
Первое уравнение - это эллипс, его уравнение линии 2-го порядка задано общим видом Ax² + 2Bx + Cy² + 2Dx + 2Ey + F = 0.
Продольная ось повёрнута от оси Ох на угол, определяемый по формуле tg(2α) = 2B/(A - C) = -42/(9 - 52) = 0,976744186 .
Угол поворота равен 22,163 градуса.
Угол наклона прямой, пересекающей эллипс равен arc tg(3/7) = 23,19859051 градуса.
Во вложении дан график эллипса и прямой.
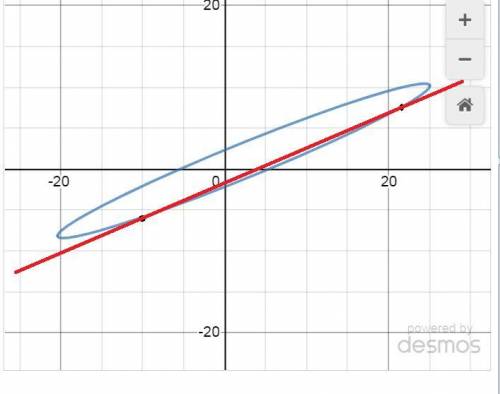
Объяснение:
у=2х+3 и у=2х+7 к1=к2, в1не равно в2 - прямые параллельные
у=3х - 4 у=6х+9 к1 не равно к2 прямые пересекаются
это то ,что касается твоих 1) и 2) пунктов.
теперь будем строить графики.Для построения прямой(а именно она яв-ся графиком линейной функции)достаточно построить 2 точки и провести через них прямую.Подставляем в функцию вместо Х какое нибудь число(самое удобно сначала подставить 0)и посчитать У.Остальное буду делать внизу.Графики построила,где что непонятно-пиши.
Объяснение:
1)12a-7
2)-2x^2+7x
3)c(10-11b)
4)2x
5)13y+5y^3
6)2c^3
7)4c+28x
8)16x-26y
9)6+b
10)12c+9x