Периметр — сумма длин всех сторон.
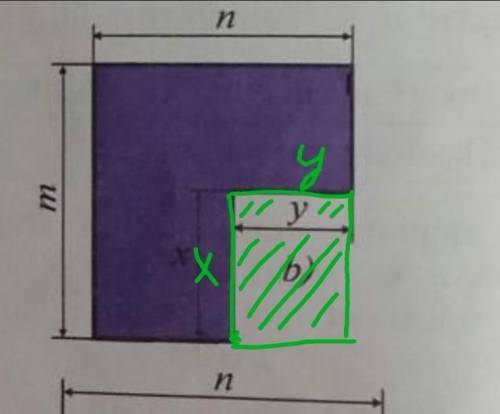
b) P = m + n + (m - x) + y + x + (n - y) = m + n + m - x + y + x + n - y = 2m + 2n
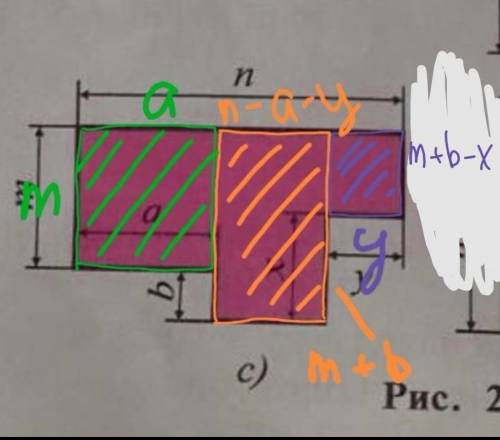
c) P = m + n + ((m + b) - x) + y + x + (n - a - y) + b + a = m + n + m + b - x + y + x + n - a - y + b + a = 2m + 2n + 2b
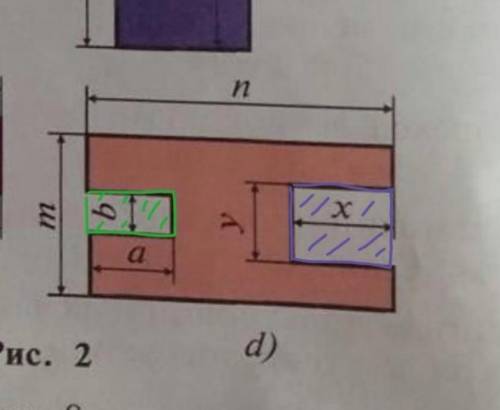
d) P = n + (m - y) + x + y + x + n + (m - b) + a + b + a = n + m - y + x + y + x + n + m - b + a + b + a = 2n + 2m + 2x + 2a
Площадь.
b) из площади общей фигуры вычтем площадь нижнего "прямоугольника". <приложение3>
S = (m × n) - (x × y) = mn - xy
с) разбиваем на три прямоугольника, площадь которых находится произведением смежных сторон. <приложение1>
S = (m × a) + ((n - a - y) × (m + b)) + (y × (m + b - x)) = am + nm + bn - am - ab - my - by + my + by - xy = nm + bn - ab - xy
d) из площади общей фигуры вычтем площади "вырезов". <приложение2>
S = (m × n) - (a × b) - (x × y) = mn - ab - xy
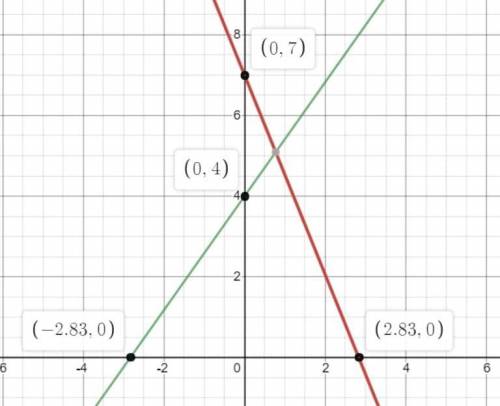
Перенесем все на координатную плоскость. Пусть точка Н = (0,0), точка А лежит на оси Оу. На скрине А(0,7), В(0,4), а рассматривать мы будем любые А(0, а) и В(0,b).
Получается, одна прямая проходит точку А и точку (-k, 0) а другая - B и (k,0), при чем мы рассматриваем всевозможные k. Здесь k - расстояние от точки Н до точки С и D.
Кстати говоря, условие, что точка В должна быть между А и Н необязательно, можно взять и точку А между В и Н, на решение это не влияет в силу симметриии, главное, что бы обе точки лежали на перпендикуляре (то есть на оси Оу).
Запишем уравнение прямых.
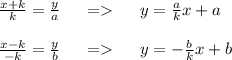
Так как нас интересует пересечение - приравниваем:
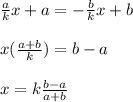
Поскольку пересечение двух прямых точно лежит на каждой из них, нужно подставить полученный икс в уравнение любой из прямых, результат будет одинаков.
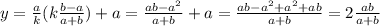
Получилось, что для любого k, то есть для любого расстояния между точкой H до С и D, мы находим зависимый от k икс, и независимый от k игрек. То есть как бы мы не раздвигали точки C и D, игрек будет всегда один и тот же, зависящий только от точек А и В, на которые мы "привязываем" прямые AD и BC.
Итого, ответ - прямая