1)Пусть катеты х см и у см.Тогда,если периметр 40,а гипотенуза 17,то х+у=40-17=23,а
у=23-х.По теореме Пифагора x^2-(23-x)^2=17^2
x^2-23x+120=0
если x=15 ,то у=8 и наоборот.
2)Обозначим производительность первой трубы через х,а второй-через у.При этом выполненную работу принимаем за 1.Работая вместе,(х+у),вся работа выполнена за 4 часа: 1/(х+у)=4.
Работая отдельно,вторая труба наполняет дольше,чем первая на 6 часов.Тогда время работы второй трубы найдем,как 1/у,а первой- 1/х и (1/у)-(1/х)=6
Решаем систему
4х+4у=1 х=1/4-у ... 24у^2-14y+1=0
х-у=6ху 1/4-у-у=6у(1/4-у) ... у(1)=1/2 НЕ
УДОВЛЕТВОРЯЕТ УСЛ.ЗАДАЧИ,у(2)=1/12,тогда х(2)=1/4-1/12=1/6 это производительности второй(у2) и первой(х2) труб.А чтобы узнать время работы первой трубы,надо работу(единицу) разделить на производительность,т.е.
1/( 1/6)=6(часов) первая труба самостоятельно наполнит бассейн
1)19,71293
округляем до сотых: 19,71
Абс. погрешность = |19.71 - 19.71293| = 0.00293
2)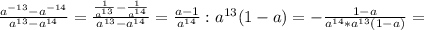

3)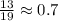
Абс. погрешность =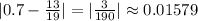
Отн. погрешность =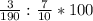 2.26%
2.26%