Объяснение:
Задачу можно решить различными .
. Первого игрока команды можно выбрать среди 15 спортсменов, то есть . Второго игрока команды можно выбрать среди оставшийся 14 спортсменов, то есть . Точно также, третьего игрока команды можно выбрать , четвёртого игрока команды можно выбрать , и наконец, пятого игрока команды можно выбрать .
Однако каждая команда при этом подсчете учтена несколько раз: одна и та же пятёрка спортсменов может быть выбрана по разному, например, сначала А, потом В, потом С, потом D, потом E, или сначала B, потом А, потом C, потом D, потом E и так далее. Поскольку число перестановок из пяти элементов равно 5!=120, то каждая команда учтена нами ровно 120 раз. Поэтому получается, что команду из 5 игроков можно выбрать
.
. Применим формулу комбинаторики.
Определение. Пусть имеется множество, содержащее n элементов. Произвольный неупорядоченный набор, состоящий из k различных элементов данного множества, называется сочетанием из n элементов по k элементов (или просто сочетанием из n по k).
Число сочетаний из n элементов по k элементов обозначается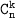 
и вычисляется по формуле:
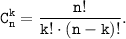
Так как n = 15 и k = 5, то
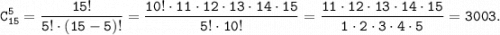
Область определения - это допустимые значения Х -обозначается D(y)/.
а) прямая - Х любое или D(y) - Х∈(-∞; +∞)
б) квадратичная функция - Х∈R или Х∈(-∞; +∞) - Х любое.
в) Если У= 2х/( 5 - х), то все кроме Х = 5 - деление на 0 не допускается - значение Х=5 исключается.
Записывается D(y)- Х∈(-∞;5)∪ (5;+∞)
Внимание: Х=5 не может быть - обозначаем круглой скобкой.
г) Произведение двух чисел. Х = любое.
д) У = 1/х² +1 - Все кроме Х=0 - деление на 0.
Х ∈ (-∞;0)∪(0;+∞)
е) Квадратный корень не может быть из отрицательного числа. Х ≥0.
D(y) - X∈[0;+∞).
Внимание: значение Х=0 может быть - в записи квадратная скобка.
Объяснение: