Для начала вспомним т. Виетта
для уравнения вида x²+px+q=0
выпоняется : x₁+x₂= -p; x₁*x₂=q
теперь решение:
1) x²-13x+q=0
x₁=12.5
x₁+x₂= -(-13)=13
12.5+x₂=13
x₂=0.5
x₁*x₂=12.5*0.5=6.25= q
тогда уравнение будет x²-13x+6.25=0
2) 10x²-33x+c=0
приведем его к стандартному виду
x²-(33/10)x+(c/10)=0
x²-3.3x+(c/10)=0
x₁=5.3 тогда 5.3+x₂=3.3; отсюда x₂= -2
c/10=5.3*(-2)=-10.6; Значит с= -106
Уравнение будет иметь вид 10x²-33x-106=0
3) x²+2x+q=0
x₁²-x₂²=12
(x₁-x₂)(x₁+x₂)=12
(x₁-x₂)*(-2)=12
x₁-x₂= -6
x₁=x₂-6
Теперь найдем корни
x₁+x₂=x₂-6+x₂=-2
2x₂=4
x₂=2; x₁= -4
тогда q=2*(-4)= -8
Уравнение примет вид x²+2x-8=0
его корни x₁²-x₂²=(-4)²-(2)²=16-4= 12
A1: x=3
A2: 8
A3: 0,8
A4: 4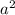 - 49
- 49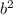
В1:3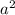 + 5
+ 5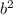
B2: 4,2 | 22,2
С: x = 2
Объяснение:
A1:
3x - 2 = x + 4
2x = 6
x =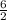 = 3
= 3
A4:
(2a - 7b)*(2a + 7b) = 4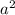 - 49
- 49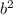 (Формула сокр. умножения)
(Формула сокр. умножения)
B1:
а(3a + 2b) – b(2a – 5b) = 3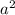 + 2ab - 2ab + 5
+ 2ab - 2ab + 5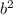 = 3
= 3
B2:
у = 0,5x – 7,1
1) -5 = 0,5x - 7,1; 2,1 = 0,5x; x = 4,2:
2) 4 =0,5x - 7,1; 11,1 = 0,5x; x = 22,2
C:
(x – 2)2 + 3x – 6 – 5(2 – x) = 0
2x - 4 +3x - 6 - 10 + 5x = 0
10x = 20
x = 2
A2:
A3:
4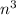 * 0,2
* 0,2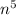 = 0,8
= 0,8 (4*0,2 и сложение степеней n)
(4*0,2 и сложение степеней n)