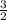 (можем перевести в десятичную дробь =1,5)
(можем перевести в десятичную дробь =1,5)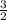 или 1,5
или 1,5Для решения задачи через квадратное уравнение, необходимо обозначит скорость течения реки как х км/ч.
В таком случае, скорость теплохода по течению будет равна: (18 + х) км/ч.
Скорость теплохода против течения реки составит: (18 - х) км/ч.
Получим уравнение суммы времени.
(50 / (18 + х)) + (8 / (18 - х)) = 3
900 - 50 * х + 144 + 8 * х = -3 * х^2 + 972.
3 * х^2 - 42 * х + 72 = 0.
х^2 - 14 * х + 24 = 0.
Д^2 = (-14)^2 - 4 * 1 * 24 = 196 + 96 = 100.
Д = 10.
х = (14 - 10) / 2 = 4 / 2 = 2 км/ч.
Скорость течения реки 2 км/ч.
3. Пусть A(x; y) - заданная точка.
По условию y = 3. Чтобы найти x, нужно y подставить в уравнение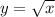 :
:
Очевидно, что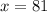 , поскольку
, поскольку 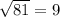
ОТВЕТ: 81.
5. Очевидно, что общее число процентов должно равняться 100.
Пусть искомая относительная частота равна х.
Тогда 4 + 0 + 8 + x + 12 + 24 + 20 + 16 + 4 = 100;
x + 88 = 100 ⇒ x = 12.
ОТВЕТ: 12%.
6. Упростим выражение:
Подставляем b= 3,75:
ОТВЕТ: -8.
7. Упростим отдельно числитель и знаменатель:
ОТВЕТ: (x²y)/4
8. Пусть x км/час - скорость почтового поезда. Тогда скорость скорого поезда - (x + 20) км/час.
Время, которое затратит скорый поезд на 280 км, равно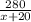 , а время, которое затратит почтовый поезд на 300 км, равно
, а время, которое затратит почтовый поезд на 300 км, равно 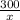 .
.
По условию время , затраченное почтовым поездом, на 2 часа больше, чем время, затраченное скорым, поездом, т.е. имеем уравнение
По теореме Виета находим два корня: x = -60 и x = 50. Очевидно, первый по смыслу задачи не подходит, поэтому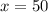 (км/час) - искомая скорость почтового поезда.
(км/час) - искомая скорость почтового поезда.
ОТВЕТ: 50 км/час.