1) х + (2х + 0,5) = х + 2х + 0,5 = 3х + 0,5.
2) 3х - (х - 2) = 3х - х + 2 = 2х + 2.
3) 4а - (а + 6) = 4а - а - 6 = 3а - 6.
4) 6b + (10 - 4.5b) = 6b + 10 - 4.5b = 1.5b + 10.
Объяснение:
Упростим выражения.
1) х + (2х + 0,5) = х + 2х + 0,5 = 3х + 0,5.
2) 3х - (х - 2) = 3х - х + 2 = 2х + 2.
3) 4а - (а + 6) = 4а - а - 6 = 3а - 6.
4) 6b + (10 - 4.5b) = 6b + 10 - 4.5b = 1.5b + 10.
Для того, чтобы упростить данное выражение, мы в первую очередь раскрыли скобки. Если перед скобками стоит знак минус, то при раскрытии скобок мы меняем знаки членов в скобках на противоположные. Затем мы сгруппировали члены, которые содержат неизвестное и свободные члены.
а) n-ый член геометрической прогрессии ищется по формуле:
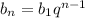
Тогда пятый член этой прогрессии равен:

б) Аналогично по формуле n-го члена геом. прогрессии вычисляем девятый член прогрессии:
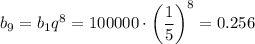
в) Сумма первых n членов геометрической прогрессии ищется по следующей формуле:
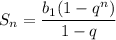
Тогда сумма первых восьми членов этой прогрессии равна:

г) Аналогично с в) по формуле суммы n первых членов геометрической прогрессии вычисляем сумму первых пяти членов этой прогрессии:
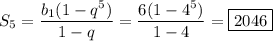
д) Предполагается, что нужно найти сумму бесконечно убывающей геометрической прогрессии:

Тогда
А) -36; - 12; -4;
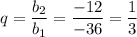
Сумма бесконечно уб. г.п. 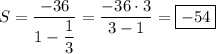
Б) 
Сумма бесконечно убывающей геометрической прогрессии:
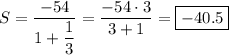
e) используя n-ый член геометрической прогрессии, рассмотрим пятый член этой прогрессии:
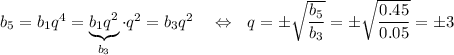
Так как по условию q>0, то q=3
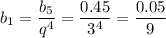
Сумма первых восьми членов этой прогрессии равна:

Объяснение:
1)
x²+5x+4≥0
x²+4x+x+4≥0
x*(x+4)+(x+4)≥0
(x+4)(x+1)≥0
-∞__+__-4__-__-1__+__+∞
ответ: x∈(-∞;-4]U[-1;+∞).
2)
|2x-1|<|x+1|
Подмодульные выражения равны нулю, если:
2х-1=0 2x=1 |÷2 x=1/2
x+1=0 x=-1 ⇒
x∈(-∞;-1]
-(2x-1)<-(x+1)
-2x+1<-x-1
x>2 ∉.
x∈[-1;1/2]
-(2x-1)<x+1
-2x+1<x+1
3x>0 |÷3
x>0 ⇒
x∈(0;1/2]
x∈[1/2;+∞)
2x-1<x+1
x<2 ⇒
x∈[1/2;2)
ответ: x∈(0;2).
3)
(x-4)²*(x²-8x)<0
Так как (х-4)²≥0 ⇒
x²-8x<0
x*(x-8)<0
-∞__+__0__-__8__+__+∞
ответ: x∈(0;8).
4)
ОДЗ: 5х+3≠0 х≠-0,6
-∞__+__-0,6__-__0,5__+__+∞
ответ: х∈(-∞;-0,6)U[0,5;+∞).