Question

Розв'яжіть рівняння:
³√(х²-4х+4)+2³√(х-2)-3=0

Answer 1

х=3 или х=-25

Объяснение:

Обозначим (х-2)^(1/3)=y

y^2+2y=3  y^2+2y+1=4  (y+1)^2=2^2   y1=1 y2=-3

В первом случае   х-2=1 х=3

во втором х-2=-27  х=-25

Answer 2

-25; 3

Объяснение:

$\sqrt[3]{ {x}^{2} - 4x + 4} + 2 \sqrt[3]{x - 2} - 3 = 0 \\ \sqrt[3]{(x - 2) {}^{2} } + 2 \sqrt[3]{x - 2} - 3 = 0$

Замена:

$\sqrt[3]{x - 2} = t$

, t - любое число.

${t}^{2} + 2t - 3 = 0 \\ {t}^{2} - t + 3t - 3 = 0 \\ t(t - 1) + 3(t - 1) = 0 \\ (t - 1)(t + 3) = 0 \\ t = 1 \\ t = - 3$

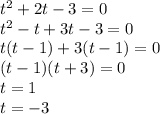
Обратная замена:

1)

$t = 1 \\ \sqrt[3]{x - 2} = 1 \\ x - 2 = 1 \\ x = 3$

2)

$\sqrt[3]{x - 2} = - 3 \\ x - 2 = - 27 \\ x = - 25$

Уравнение решено!