х = -2; у = 3
или
(-2; 3)
Объяснение:
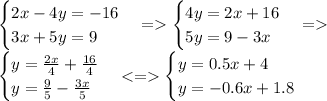
Построим графики полученных уравнений: мы привели их к виду уравнения прямой
у = kx + b,
k - тангенс угла наклона прямой
b - смещение графика от (0,0) вдоль оси Оу
Построили. См рис.
(Пояснения: рядом с самими графиками написаны исходные уравнения, данные в условии. Внизу же, под сеткой координат - записаны функции вида у = kх + b. В принципе, это одно и то же)
Очевидно, решением системы будет точка пересечения графиков функций.
В нашем случае точка пересечения имеет координаты
х = -2; у = 3
или
(-2; 3)

Построим график функции у = 8 + 2x - x²
Для этого преобразуем её к виду
у = -(х² - 2х + 1) + 9
у = -(х - 1)² + 9
Видим, что парабола у = -х² сдвинута по оси абсцисс на 1 вправо и на 9 вверх. То есть её вершина находится в точке с координатами (1; 9).
Найдём координаты точек пересечения параболы с осью ординат.
При х = 0 у = 8
И координаты точек пересечения параболы с осью абсцисс
у = 0
- х² + 2х + 8 = 0
D = 2² - 4 · (-1) · 8 = 36
√D = 6
х₁ = -0,5(-2 - 6) = 4
х₂ = -0,5(-2 + 6) = -2
Итак мы получили ещё две точки параболы (4; 0) и (-2; 0).
Строим параболу (веточки её опущены вниз).
Смотри прикреплённый рисунок.
1) по графику видим, что функция убывает на интервале х ∈ [1; +∞)
2) множество решений неравенства 8 + 2x - x^2 ≤ 0 есть объединение двух интервалов х∈ (-∞; -2] ∪ [4; +∞)
2.42+7.7+9/1.331-1 + 4.4+3/1.21+1.1+1 - 5/1.1-1 = 191.2/3.31 + 7.7/3.31 - 50 = 191.2+7.7/3.31 - 50 = 198.9/3.31 - 50*3.31 = 198.9-165.5/3.31 = 34.4/3.31 = 3340/331
Объяснение: