≈ 24,6°
Объяснение:
Для начала найдем вектор по координатам точек:
AB = {Bx - Ax; By - Ay; Bz - Az}
AB = {3 - 3; -2 - (-1); 2 - (-3)}
AB = {0; -1; 5}
CD = {Dx - Cx; Dy - Cy; Dz - Cz}
CD = {1 - 2; 2 - (-2); 2 - 3}
CD = {-1; 4; -1}
Теперь найдем скалярное произведение векторов:
AB · CD = ABx · CDx + ABy · CDy + ABz · CDz
AB · CD = 0 · (-1) + (-1) · 4 + 5 · (-1)
AB · CD = 0 - 4 - 5
AB · CD = -9
Затем найдем длины векторов:
|AB| =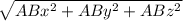 
|AB| =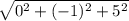 
|AB| =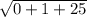 
|AB| =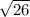 
|CD| =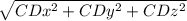 
|CD| =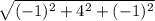 
|CD| =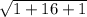 
|CD| =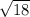 
|CD| = 3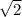
Найдем косинус угла между векторами:
cos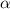 
= 
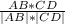
cos =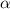 
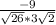
cos =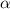 
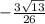
cos 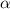= ≈ -0.41602514716892186
И наконец-то находим по таблице брадисса угол, с найденого косинуса
Это ≈ 24,6°
Объяснение:
Коэффициент равен (У2-У1)/(Х2-Х1)=()()
Даны по две точки на каждой функции
(0;5 ) и (7,5;0) на первой (У2-У1)/(Х2-Х1)=(0-5)(7,5-0)=-5/7,5=-2/3
У=аХ+в; 0=-2/3*7,5+в; 0=-5+в; в=5
У=-2/3 Х+5
(-2;-1)(1;0 .)на второй. (У2-У1)/(Х2-Х1)=(0-(-1))(1-(-2))=1/3
У=аХ+в; 0=1/3*1+в; 0=1/3+в; в=-1/3
У=1/3 Х-1/3
Система уравнений
У=-2/3 Х+5
У=1/3 Х-1/3 *2
У=-2/3 Х+5
+
2У=2/3 Х-2/3 получим 3У=5-2/3 3у=4 1/3 У=13/9 У=1 4/9
1 4/9 = 1/3*Х -1/3 13/9 = 1/3*Х -3/9
16/9=1/3 Х
16/3=Х
5 1/3=Х ( 5 1/3; 1 4/9)
ответ: 80m-5m^5
Объяснение:
5m*(4+m^2)*(4-m^2)
5m*(16-m^4)