Объяснение:
1) Сложить числа 27+9 : a3 +36 + a2 - 3a
2)Используем переместительный закон : a3 + a2 - 3a + 36
3)Записываем a2 в виде разности : a3 + 4a2 - 3a2 - 3a + 36
4) Записываем -3a в виде суммы : a3 + 4a2 - 3a2 - 12a + 9a + 36
5) Выносим за скобки общий множитель a2 : a2 × (a+4) - 3a2 - 12a + 9a + 36
6) Выносим за скобки общий множитель -3a : a2 × (a+4) - 3a ×(a+4)+ 9a +36
7) Выносим за скобки общий множитель 9 : a2 × (a+4) - 3a × (a +4)+ 9×(a+4)
8)Выносим за скобки общий множитель a+4 : (a+4)×(a2-3a + 9)
ответ : (a+4) ×(a2-3a +9)
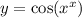
Мы видим, что данная функция является сложной, поэтому будем её дифференцировать как сложную.
Формула
d/dx( f(g(x)) ) = f'(g(x)) × g'(x), где в нашем случае f(x) = cos(x), а g(x) = x^x.
Для применения правила дифференцирования сложной функции, заменим x^x новой переменной t.
Дифференцируем
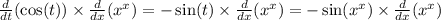
Для упрощения производной запишем х^х как e^( ln(x^x) ).
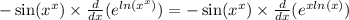
И опять сложная функция.
Дифференцируем её аналогично:
f(x) = e^x, g(x) = xln(x)
Заменим xln(x) перевенной k:
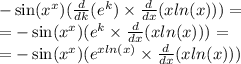
За правилом производной произведения имеем:
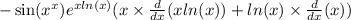
Вычисляем все производные и получаем:
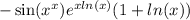
Это и есть ответ.
ответ: майстру потрібно 24 години, учню 48 год
Объяснение: Нехай майстру потрібно х год, тоді учню потрібно х+24 год. За одну годину разом вони виконують 1/16 роботи. Майстер виконує 1/х роботи за годину, відповідно учень 1/х+24 за годину
Маємо рівняння:
1/х+24+1/х=1/16
х≠-24
х≠0
16х+16*(х+24)-х*(х+24)/16х*(х+24)=0
16х+16х+384-х²/16х*(х+24)=0
х²-8х-384=0
х*(х+16)-24*(х+16)=0
(х+16)*(х-24)=0
х+16=0 і х-24=0
х=-16 це сторонній корінь,
х=24(год) - час за який майстер виконує цю роботу
х+24=24+24=48(год) - час за який учень виконує цю роботу
Відповідь: 24 год, 48 год