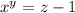
Любое простое число, кроме 2, является нечётным.
Если z = 2, то либо x = 1, либо y = 0. Оба из этих чисел не являются простыми. Значит, z ≠ 2.
Если z — число нечётное, то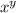 
— чётное. Учитывая, что x и y — простые числа, x может быть равен только 2, иначе это будет нечётным числом.
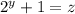
Попробуем поперебирать значения y:
2² + 1 = 5 — подходит,
2³ + 1 = 9 — не подходит,
2⁵ + 1 = 33 — не подходит,
2⁷ + 1 = 129 — не подходит...
Можно заметить, что при нечётных y z делится на 3. Всегда ли выполняется это условие?
Множество нечётных чисел включает в себя множество простых чисел (за исключением 2). Если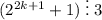 
, то и для простых чисел, кроме 2, это тоже справедливо.
Докажем это методом математической индукции:
1. При k = 1 утверждение верно (см. перебор, второе равенство).
2. Пусть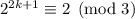 
— верно.
3. 
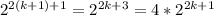
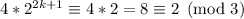
Значит, 2 в любой нечётной степени (даже 2¹, которое мы упустили из доказательства) при делении на 3 даёт остаток 2. Отсюда справедливо выражение 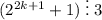. Значит, z при всех простых y, отличных от 2, делится на 3, то есть не является простым числом. Отсюда получаем единственное найденное решение: x = 2, y = 2, z = 5.
ответ: (2; 2; 5)
Объяснение:
1) Завдання
Пусть х буде перше число, тоді друге у.
Сума їх дорівнює 70, тобто х+у=70
А різниця 28, тобто х-у=28
Складаємо систему рівнянь
{х+у=70
х-у=28
Метод додавання
2х=98
х=98:2
х=49 перше число
Підставляємо значення х в одно із рівнянь
х+у=70
49+у=70
у=70-49
у=21 друге число
Відповідь: (49;21)
2) завдання
Пусть х буде коштувати 1 ручка, тоді у буде коштувати 1 олівець
5 ручок і 4 олівці коштують 50 грн, тобто 5х+4у=50
3 ручкі дорожче за 2 олівця на 8грн.
тобто 3х-2у=8
Складаємо систему рівнянь
{5х+4у=50
3х-2у=8 множимо на 2
{5х+4у=50
6х-4у=16
Метод додавання
11х=66
х=66/11
х=6 грн. коштує 1 ручка
Підставляємо значення х в одно із рівнянь
3х-2у=8
3*6-2у=8
18-2у=8
-2у=8-18
-2у=-10
у=10/2
у=5 грн коштує 1 олівець
Відповідь: 5грн. коштує 1 олівець, 6грн. коштує 1 ручка.