обозначим скорость лодки -X км/ч,скорость течения реки-y кмч.
за один час по течению реки туристы на моторной лодке проедут -(x+y) км
за 1/2 часа с выключенным мотором по течению реки-1/2 y
итого в одном направлении -(x+y+1/2y)км
в обратном направлении с включенным мотором против течения за 3 часа они проедут 3(x-y)км
приравниваем эти два значения (расстояние не меняется):
(x+y+1/2y)=3(x-y)
x+3/2y=3x-3y
-2x=-3y-3/2y
-2x=-9/2y
x=9/4y
x=2.25y
ответ :скорость течения реки 2.25 раз меньше собственной скорости лодки
Найти частное решение линейного неоднородного уравнения 2-го порядка.
Алгоритм решения неоднородного ДУ следующий:
1) Сначала нужно найти общее решение соответствующего однородного уравнения y``+y`-2y=0
Составим и решим характеристическое уравнение:
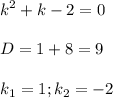
получены различные действительные корни, поэтому общее решение:
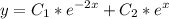
2) Теперь нужно найти какое-либо частное решение неоднородного уравнения
в правой части 4e²ˣ-2x+1. Значит предположу что частное решение неоднородного уравнения нужно искать в виде: y=Аe²ˣ+Bx+C
Найдём первую и вторую производную:
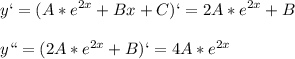
подставим в левую часть
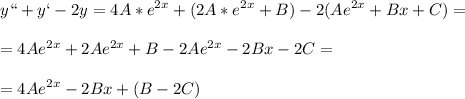
и теперь приравняем к правой
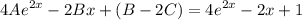
отсюда составим систему
![\displaystyle \left \{ {{4A=4; -2B=-2} \atop {B-2C=1}} \right. \]\\\\A=1; B=1;C=0](/tpl/images/3220/5151/2929a.png)
3) Запишем общее решение неоднородного уравнения:
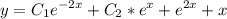
4) теперь найдем частное решение
y(0)=3; y`(0)=5
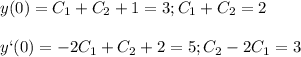
решая систему получим
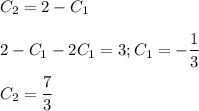
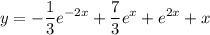
1) D(y)=(-∞; ∞), Е(у)= (-∞; 5]
2) D(y)= (-∞; 0)∪(0;+∞). график в приложении (первый график в виде параболы с ветвями вверх)
3) график тоже в приложении (второй график - в виде ломанной)
Объяснение:
1) Так как это полином, то нет особых точек функции, где она бы не существовала, значит эта функция определена на всей оси ОХ.
D(y)=(-∞; ∞).
Область значений найти несколько сложнее. Так как это парабола с ветвями, направленными вниз, то надо найти координаты вершины параболы. Координата вершины параболы ищется по формуле: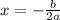 . Подставим известные данные:
. Подставим известные данные: 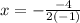 . Или
. Или 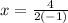 , х=-2.
, х=-2.
Тогда у(-2)=-(-2)²-4(-2)+1. у(-2)=-4+8+1. у(-2)=5. Так как это парабола с ветвями, направленными вниз, то все ее остальные значения будут меньше 5. Значит область значений меняется от (-∞) до 5 включительно.
Е(у)= (-∞; 5]. Третий график в приложении. Он подписан.
2) Если сократить числитель и знаменатель на х, то получим функцию f(x)=x²-6x+5 - обычная парабола с вершиной в точке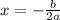 , то есть
, то есть 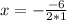 или х=3. При этом у=3²-6*3+5, то есть у=9-18+5. Или у=-4.
или х=3. При этом у=3²-6*3+5, то есть у=9-18+5. Или у=-4.
Вершина параболы в точке (3; -4). Точки пересечения с осью оХ можно найти, если функцию приравнять к нулю. То есть x²-6x+5=0. Нетрудно увидеть, что
(х-1)*(х-5)=0.
х₁=1, х₂=5 - в этих точках парабола пересекает ось ОХ. Ветви параболы направлены вверх, так как коэффициент при старшем члене равен 1>0.
В точке х=0 функция у(х) не существует, так как х, находясь в знаменателе, позволяет взять предел данной функции. Предел этой функции в точке х=0 равен значению f (x). То есть f (0)=(0-1)*(0-5),
f(0)=5. Это место на графике можно указать стрелками.
Область определения этой функции будет (-∞; 0)∪(0;+∞).
То есть D(y)= (-∞; 0)∪(0;+∞). График функции смотрите в приложении.