Question

Решите системы уравнений сложения ​

Answer 1

1. (6;-1) 2. (5; -1) 3. (-3;13) 4.(-3.5;-1) 5. (-1;2).

Объяснение:

1. Сложим 2 уравнения. y сократиться и получим:

2x=12

x=6.

Подставим полученный x=6 в любое уравнение системы (например в первое, получим уравнение относительно y , которое решим:

6+y=5;

y=5-6;

y= -1.

2. Домножим обе части первого уравнения на 5. Получим систему:

5x+5y=20;

3x-5y=20.

Сложим два уравнения, 5y и -5y сократятся дав в сумме 0.

получим уравнение относительно x:

8x=40;

x=5.

Подставляем x=5 например в первое уравнение:

5+y=4;

y=4-5;

y=-1.

3. $\left \{ {{x-y=-10}; \atop {2x+3y=15};} \right.$$\left \{ {{3x-3y=-30} \atop {2x+3y=15}} \right.$

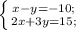
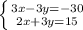
Складываем два уравнения:

5x=-15

x=-3

3-y=-10

-y=-10-3

y=10+3

y=13.

4. Первое ур-е умножим обе части на 3 а второе ур-е умножим обе части на -2.

Получим новую систему:

$\left \{ {{6x+9y=-3} \atop {-6x-10y=4}} \right.$

9y-10y=-3+4

-y=1

y=-1.

Подставляем в первое уравнение исходной системы y=2.

2x+3*2=-1

2x+6=-1

2x=-1-6

2x=-7

x=-3.5.

5. $\left \{ {{3x+2y=1} \atop {2x+5y=8}} \right.$   $\left \{ {{-6x-4y=-2} \atop {6x+15y=24}} \right.$

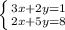
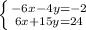
-4y+15y=-2+24;

y=2.

3x+2*2=1;

3x+4=1;

3x=1-4;

3x=-3;

x=-1.