1. У выражение (а+6)^2–а(3+а)
2. Представить в виде степени а) х5*х11*х6 б) (-3)4*(-3)5:(-3)6
3. Постройте график функции у = 2х – 2. Определите, проходит ли график функции через точку А (- 10; - 20)
4.Решите задачу с уравнения: Турист км за 3 дня. Во второй день он на 10 км меньше, чем в первый день и на 5 км больше, чем в третий день. Сколько километров проходил турист каждый день?
5.Разложите на множители: а) 49х2-100 б)12ху+15х в)9у2-16х2
6.Решите уравнение: – 5(0,2х+1)=3(3–2х)
x1+x2=-7 U x1*x2=12⇒x1=-4 u x2=-3
x²+6x+8=(x+4)(x+2)
x1+x2=-6 U x1*x2=8⇒x1=-4 U x2=-2
x²+8x+15=(x+5)(x+3)
x1+x2=-8 U x1*x2=15⇒x1=-5 U x2=-3
x²+7x+10=(x+5)(x+2)
x1+x2=-7 U x1*x2=10⇒x1=-5 U x2=-2
x²+6x+9=(x+3)²
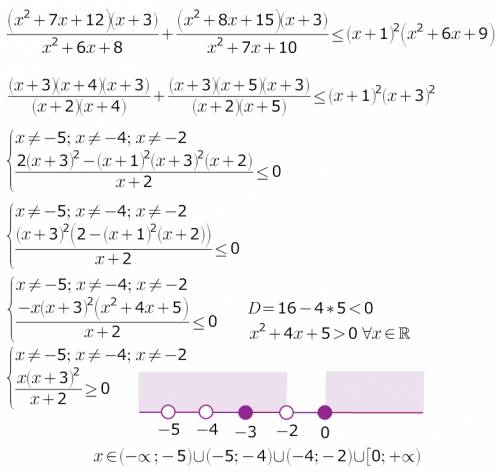
(x+4)(x+3)²/[(x+4)(x+2)]+(x+5)(x+3)²/[(x+5)(x+2)] -(x+1)²(x+3)²≤0
(x+3)²/(x+2)+(x+3)²/(x+2) -(x+1)²(x+3)²≤0,x≠-4 U x≠-5
2(x+3)²/(x+2)-(x+1)²(x+3)²≤0
(x+3)²(2-(x+2)(x+1)²)/(x+2)≤0
(x+3)²(2-x³-2x²-2x²-4x-x-2)/(x+2)≤0
(x+3)²(-x³-4x²-5x)/(x+2)≤0
(x+3)²*x*(x²+4x+5)/(x+2)≥0
x²+4x+5>0 при любом х,т.к.D<0⇒
(x+3)²*x/(x+2)≥0
x=-3 x=0 x=-2
+ + _ +
[-3](-2)[0]
x∈(-∞;-5) U (-5;-4) U (-4;-2) U [0;∞)