8<x<20 км.
Объяснение:
Пусть x км проплыли туристы по течению реки, тогда против течения они проплыли (20−x) км.
7−1 = 6 км/ч — скорость лодки против течения реки;
7+1 = 8 км/ч — скорость лодки по течению реки.
Чтобы найти время, надо расстояние поделить на скорость, поэтому:
20−x6 ч. — время, затраченное туристами на путь против течения реки;
а x8 ч. — время, затраченное туристами на путь по течению реки.
Зная, что в пути туристы были менее трёх часов, составим неравенство:
20−x6+x8<3.
Чтобы избавиться от дроби, умножим обе части неравенства на 48.
(20−x6+x8)⋅48<3⋅48;
20−x6⋅48+x8⋅48<144;
8⋅(20−x)+6⋅x<144;
160−8x+6x<144;
−2x<−16
x>8.
Правильный ответ: 8<x<20 км.
20 и 19 марок.
Объяснение:
Пусть на первой странице было x марок, а на второй странице - y марок. После того, как 35% марок с первой страницы переложили на вторую, на первой странице стало x-0,35x=0,65x марок, а на второй странице стало y+0,35x марок. По условию задачи, на второй странице марок стало в 2 раза больше, чем на первой. Тогда
2*0,65x=y+0,35x
1,3x=y+0,35x
1,3x-0,35x=y
0,95x=y
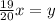
По смыслу задачи, x и y - положительные целые числа. Минимальное положительное целое значение x, при котором y также будет положительным целым, равно 20. Если x=20, 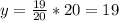 .
.
Ну вот! Удачи! Учись!
Объяснение: