я подозреваю что тут закралась неясность, в прогрессии насколько я помню количество элементов бесконечно, хотя в убывающей геометрической прогресии сумма всех элементов может сходиться.
инфми словами условие следует понимать так что n первых членов прогресии, где n = 2k,
выполняется условие в три раза больше, чем
рассмотрим это более подробно на примере первых шести элементов
Х (км/ч) - скорость лодки в стоячей воде (по озеру). х-2 (км/ч) - скорость лодки против течения. х+2 (км/ч) - скорость лодки по течению.
25(x-2)(x+2)+9x(x+2)-56x(x-2)=0 25(x²-4)+9x²+18x-56x²+112x=0 25x²-100-47x²+130x=0 -22x²+130x-100=0 11x²-65x+50=0 D=65²-4*11*50=4225-2200=2025=45² x₁=(65-45)/22=20/22=10/11 - не подходит, так как скорость лодки меньше скорости течения реки - лодка не сможет плыть против течения, ее будет сносить. х₂=(65+45)/22=110/22=5 (км/ч) - скорость лодки в стоячей воде. ответ: 5 км/ч.
я подозреваю что тут закралась неясность, в прогрессии насколько я помню количество элементов бесконечно, хотя в убывающей геометрической прогресии сумма всех элементов может сходиться.
инфми словами условие следует понимать так что n первых членов прогресии, где n = 2k,
выполняется условие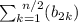 в три раза больше, чем
в три раза больше, чем 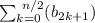
рассмотрим это более подробно на примере первых шести элементов
сумма нечетных S(1,3,5) = b1 + b3 + b5
сумма четных S(2,4,6) = b2 + b4 + b6 = b1*q + b3*q + b5*q = q(b1 + b3 + b5) = q*S(1,3,5)
следовательно отношение между четной суммой и нечетной равно знаменателю прогрессии.
Для нашей задачи это число 3
ответ 3