На некоторых деревьях в волшебном лесу растут монеты. Деревьев, на которых вообще не растут монеты, в два раза больше, чем деревьев, на которых растут по три монеты. На трёх деревьях растут по 22 монеты, на четырёх деревьях — по 44 монеты, а больше, чем по 44 монеты, ни на каком дереве не растёт. На сколько общее число монет в волшебном лесу больше, чем число деревьев?
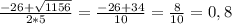

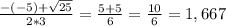

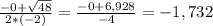
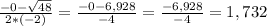
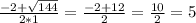
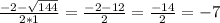
2т^2-кт+4=0
8т^2-2кт+4=0
-4т^2+2кт-8=0
8т^2-2кт+4=0
4т^2-4=0
2т^2-кт+4=0
т=1 или т= -1
Если т=1 то к=6,
если т= -1 то к= -6.
Таким образом получили 2 случая:
1) при к=6 корни уравнения ( т и 2т ) равны 1 и 2
2) при к= -6 корни уравнения ( т и 2т ) равны -1 и -2
ответ: к=6, х1=1, х2=2 или к= -6, х1= -1, х2= -2