1. Т.к. в линейном выражении 1-2у перед у стоит знак "-", то при вычислении пределов возможных значений нужно либо поменять направление знаков больше (меньше) либо поменять местами подставляемые значения 1/2 и 8.
для 1/2 ≤ у: 1-2у ≤ 0
для у ≤ 8: 1-2у ≥ -15
Тогда: -15 ≤ 1-2у ≤ 0
2. Здесь перед у знак "+", но появилась нелинейная зависимость 4/у, поэтому нужно вычислить производную функции (4/у + у) и приравнять её к нулю, чтобы найти ее экстремум.
Но так как значение -2 не попадает в наш промежуток по условию, то это значение отбрасываем.
Значит, в точке у=2 имеем экстремум. Определим его значение:
для у=2: .
На остальных участках функция либо возрастает, либо убывает. подставим граничные значения из условия:
1.6-\3.3-х\>0 1)-\3.3-х\>-1.6 | :(-1) \3.3-х\< 1.6. 3.3-х<1.6 или 3.3-x>-1.6 х<1.7 х>4.9 рисуем прямую и на ней отмечаем точки 1.7 и 4.9 незакрашенными, ибо нер-во строгое. http://cs623230.vk.me/v623230379/4bc09/MlpcdUa1yZE.jpg
если не отобразился рисунок мой с ссылкой, то тогда мы отмечаем штрихами от начала до 1.7 прерываем и дальше штрихи идут от 4.9 и до конца прямой. итак,ответ: функция возрастает при х = (-&;1.7.)U(4.9;+&) , функция убывает при х = (1.7;4.9). всё
1. -15 ≤ 1-2у ≤ 0
2.
Объяснение:
1. Т.к. в линейном выражении 1-2у перед у стоит знак "-", то при вычислении пределов возможных значений нужно либо поменять направление знаков больше (меньше) либо поменять местами подставляемые значения 1/2 и 8.
для 1/2 ≤ у: 1-2у ≤ 0
для у ≤ 8: 1-2у ≥ -15
Тогда: -15 ≤ 1-2у ≤ 0
2. Здесь перед у знак "+", но появилась нелинейная зависимость 4/у, поэтому нужно вычислить производную функции (4/у + у) и приравнять её к нулю, чтобы найти ее экстремум.
Но так как значение -2 не попадает в наш промежуток по условию, то это значение отбрасываем.
Значит, в точке у=2 имеем экстремум. Определим его значение:
для у=2: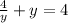 .
.
На остальных участках функция либо возрастает, либо убывает. подставим граничные значения из условия:
для у=1/2 :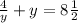
для у=8: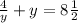 .
.
Т.е. имеем кривую с максимумами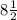 и минимумом 4.
и минимумом 4.
Тогда