Пусть скорость течения реки х, тогда время затраченное на путь по течению реки равно
40/(18+х),
а на путь против течения реки
16/(18-х).
Весть путь лодка за 3 часа, значит можно записать уравнение:
40/(18+х)+16/(18-х)=3
40*(18-х)+16*(18+х)=3*(18-х)(18+х)
720-40х+288+16х=3*(18²-х²)
1008-24х=972-3х²
3х²-24х+36=0
D=(-24)²-4*3*36=576-432=144
x₁=(24-12)/2*3=2
x₂=(24+12)/2*3=6
По условию скорость реки меньше 4 км/ч, значит выбираем корено уравнения х₁=2.
ответ: скорость реки 2 км/ч
Применим формулу сокращённого умножения:
a² - b² = (a - b)·(a + b).
1) 9·x²-4·y²-3·x+2·y = (3·x)²-(2·y)²-(3·x-2·y) = (3·x-2·y)·(3·x+2·y) - (3·x-2·y) =
= (3·x-2·y)·(3·x+2·y-1);
2) 81 - (3-8·y)² = 9² - (3-8·y)² = (9-(3-8·y))·(9+(3-8·y)) = (9-3+8·y)·(9+3-8·y) =
= (6+8·y)·(12-8·y) = 2·(3+4·y)·4·(3-2·y) = 8·(3+4·y)·(3-2·y);
3) 36-(y+1)² = 6²-(y+1)² = (6-(y+1))·(6+(y+1)) = (6-y-1)·(6+y+1) = (5-y)·(7+y);
4) (4-5·x)²-64 = (4-5·x)²-8² = (4-5·x-8)·(4-5·x+8) = (-4-5·x)·(12-5·x) =
= -(4+5·x)·(12-5·x) = (4+5·x)·(5·x-12).
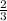от того, что осталось после первого деня, то после второго дня работы осталась 
от того, что осталось после первого дня работы. По условию, после двух дней работы осталось 2 банки, соответственно =2, из чего следует, что во второй день израсходовали 4 банки с краской (так как 2×2=4). По условию сказано, что в первый день израсходовали половину всех банок +1. Значит, 4 банки - это половина всех банок -1. Соответственно, половина - это 4+1=5. В первый день израсходовали 5+1=6 (банок с краской), во второй день израсходовали 4 (банки с краской), а осталось на третий день еще 2 (банки с краской). Суммируем все количество банок: 6+4+2=12.
2 км/ч
Объяснение:
Скорость течения реки-х
Время в пути по течению реки - 40/(18+х),
Время в пути против течения реки - 16/(18-х).
Весть путь лодка за 3 часа
Составим уравнение
40/(18+х)+16/(18-х)=3
40*(18-х)+16*(18+х)=3*(18-х)(18+х)
720-40х+288+16х=3*(18²-х²)
1008-24х=972-3х²
3х²-24х+36=0
D=B^2-4ac=(-24)²-4*3*36=576-432=144
x₁=(24-12)/2*3=2км/ч -верно, тк по условию скорость реки меньше на 4 км/ч
x₂=(24+12)/2*3=6км/ч - не верно